

 |
Elemente der Programierung |
|
Algorithmen sind aus dem Alltag nicht mehr wegzudenken, denn schon seit jeher hat der Mensch bei Problemstellungen den Wunsch, einfache, klare und eindeutige Handlungsanweisungen oder "Rezepte" zur Lösung zu finden, auszuführen und zu notieren. Insbesondere in der modernen, technisierten Welt kommen diesen Handlungsvorschriften immer größere Bedeutung zu. Neben Gebrauchsanweisungen und Kochrezepten findet man auch Montageanleitungen für Regale und Regelwerke für Sport und Spiel. Eine nicht mehr wegzudenkende Bedeutung kommt jedoch den Computeralgorithmen in der digitalen Welt zu: Im Navigationsgerät findet ein Algorithmus den kürzesten Weg, Rechtschreibalgorithmen verbessern Rechtschreib- und Grammatikfehler, im Onlinehandel schlagen Algorithmen interessante Produkte vor und auf Dating-Platformen empfehlen sie uns einen passenden Partner. Vor allem die Kombination von Algorithmen mit ungeheurlichen Datenmengen lässt ihren Einfluss und ihre Stärke weiter wachsen.
Algorithmen geben eine Vorgehensweise bzw. ein Lösungsplan zur Lösung eines Problems vor. In der Informatik bilden sie die Grundlage der Programmierung. Dabei besitzen sie ganz allgemein folgende charakteristische Eigenschaften:
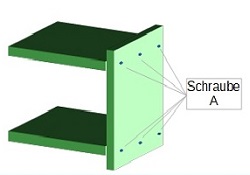
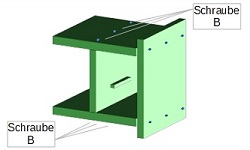
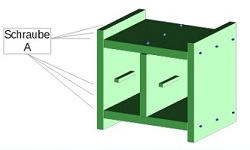
Beispiel für einen Algorithmus: Montageanleitung
 |
 |
 |
 |
Eigenschaften von Algorithmen:
Endlichkeit:
Ein Algorithmus besteht aus einer endlichen Anzahl von Anweisungen und besitzt eine endliche Länge. Demzufolge besteht auch der Quelltext des Algorithmus aus einer begrenzten Anzahl von Zeichen. Des weiteren soll ein Algorithmus nach endlich vielen Schritten anhalten oder kontrolliert abbrechen. Zu vermeiden sind Algorithmen, die zu keinem Ergebnis oder Resultat kommen und sich in Endlosschleife verlieren. Außerdem darf ein Algorithmus zu jedem Zeitpunkt nur endlich viel Speicherplatz für seine Daten belegen.
"Jeder Kunde möchte in absehbarer Zeit das neu gekaufte Bücherregal aufstellen können"
Eindeutigkeit:
Bei einem Algorithmus ist zu jedem Zeitpunkt der Ausführung die nächstfolgende Anweisung eindeutig definiert und festgelegt. Außerdem liefert ein Algorithmus stets die gleichen Resultate und Ergebnisse falls er mit den gleichen Voraussetzungen gestartet wurde. Dafür muss jede Anweisung unmissverständlich formuliert sein.
"Jeder Kunde möchte nach dem Abarbeiten der Einzelschritte in der Montageanleitung das gleiche Bücherregal wie im Katalog aufstellen können."
Ausführbarkeit
Grundsätzlich muss jede einzelne Anweisung eines Algorithmus verständlich und machbar sein, das heißt, der Ausführende des Algorithmus (Mensch, Computer, etc.) muss zu jedem Zeitpunkt in der Lage sein, die Anweisung umzusetzen. Jeder Schritt des Verfahrens muss also tatsächlich ausführbar sein.
"Jeder Kunde möchte nicht bei jedem Einzelschritt überlegen, ob dieser Schritt richtig ist und wie genau er auszuführen ist um das Bücherregal aufstellen zu können."
Algorithmen sollten also möglichst knapp, aber verständlich, präzise und eindeutig verfasst werden!
Darstellung von Algorithmen:
Zu Beginn sind Programmieraufgaben immer in Umgangssprache formuliert. Ein typischer Kunde von Softwarelösungen hat beispielsweise im Normalfall keinerlei Vorerfahrung von Programmierung und beschreibt sein zu lösendes Programmierproblem in seiner eigenen Sprache. Der berufliche Alltag eines Programmierers besteht nun darin, das Ausgangsproblem zu analysieren und anschließend in eine Programmiersprache in einen passenden Algorithmus zu übersetzen.
Will man nun die Struktur eines Algorithmus darstellen, so benutzt man zur Veranschaulichung häufig sogenannte Flussdiagramme, welche die Folge der Operationen und Sequenzen bis zur Lösung der Aufgabe beschreiben. Für eine Vereinheitlichung und besseren Lesbarkeit von Flussdiagrammen ist die Bedeutung der einzelnen Symbole eines Flussdiagramms in Normen (z. B. DIN 66001) festgelegt. Flussdiagramme werden jedoch nicht nur bei der Softwareentwicklung eingesetzt, sondern auch zur Beschreibung von Arbeitsabläufen, Prozessen oder Tätigkeiten.
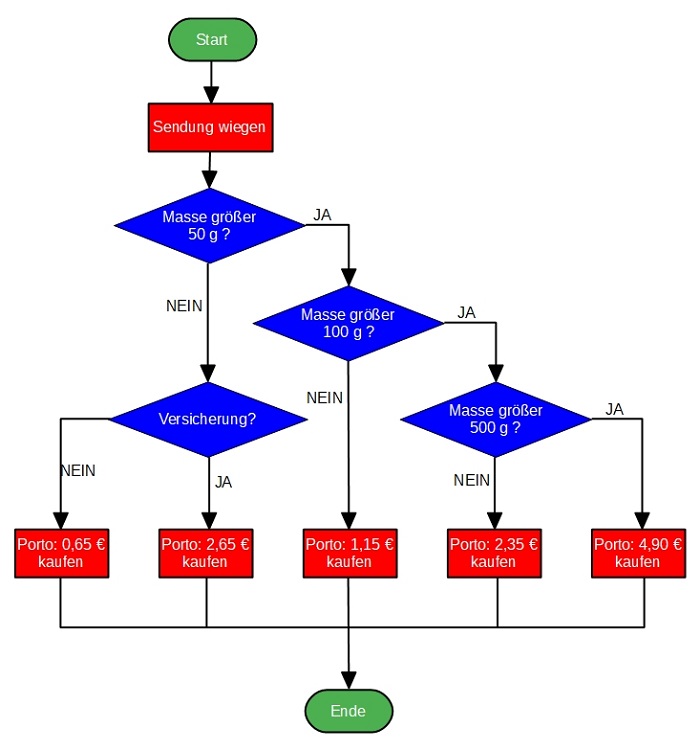 | Das Flussdiagramm zeigt, wie man das Porto für Postsendungen bestimmen kann. In einem ersten Schritt wird dazu die Sendung gewogen: Sendungen bis 50 Gramm bezeichnet man als Standardbriefe, die versichert werden können. Je nach dem beträgt das Porto 0,65 € beziehungsweise 2,65 €. Sendungen bis 100 Gramm kosten als Kompaktbriefe 1,15 €. Sendungen bis 500 Gramm werden als Großbriefe mit 2,35 € frankiert. Am teuersten sind Sendungen, die schwerer als 500 Gramm sind. Diese müssen mit einem Porto von 4,90 € frankiert werden. |

Häufig sollen bestimmte Anweisungen oder Sequenzen wiederholt ausgeführt werden. Soll beispielsweise ein Quadrat von einem Fahrroboter abgefahren werden, so wiederholt sich viermal die Sequenz: "1. Fahrt geradeaus, 2. Drehung um 90° nach rechts"
Zur Programmierung solcher Wiederholungen verwendet man Schleifen (engl. Loop). Entscheidend ist dabei, wie lange oder wie oft die Wiederholung durchgeführt wird. Dazu können sogenannte Abbruchbedingungen definiert werden, die am Ende einer jeden Wiederholung überprüft werden. Wird die gesetzte Abbruchbedingung erfüllt, so wird das Wiederholen beendet und die Ausführung der weiteren Sequenzen wird fortgesetzt.Je nach Programmiersprache sind unterschiedliche Arten von Abbruchbedingungen möglich.
Typische Schleifen:| Name | FOR-Schleife | ZEIT-Schleife | WHILE-Schleife | |
| Abbruchbedingung | Wiederholung wird beendet falls eine gewisse Anzahl von Durchläufen erreicht ist. | Wiederholung wird beendet falls eine bestimmte Zeit verstrichen ist. | Wiederholung wird beendet falls ein Ereignis eintrifft. | |
| Beispiel | Ein Leuchtdiode blinkt genau 70 mal auf. | Eine Leuchtdiode blinkt bis die Zeit von 90 Sekunden verstrichen ist. | Eine Leuchtdiode blinkt bis der Temperatursensor eine Raumtemperatur über 35°C misst. |
Grundsätzlich muss die Abbruchbedingung in der Schleife selber überprüft werden. Beim Programmieren ist darauf zu achten, dass die Abbruchbedingung prinzipiell erfüllt werden kann. Ansonsten kommt es zu Endlosschleifen, das Programm muss dann gezielt von außen beendet werden.

Zu den wichtigsten Programmstrukturen, die Einfluss auf den Programmablauf nehmen, gehören Verzweigungen (auch if-Befehle genannt). Mit Hilfe solcher Verzweigungen lassen sich Programmteile festlegen, die nur unter bestimmten Voraussetzungen oder Bedingungen ausgeführt werden. Verzweigungen reagieren beispielsweise auf bestimmte Sensorwerte oder auf berechnete interne Werte. Man kann verschiedene Arten von Verzweigungen unterscheiden:
| Einfache Verzweigung | Mehrfache Verzweigung |
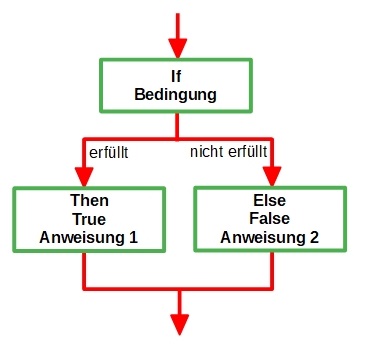 | 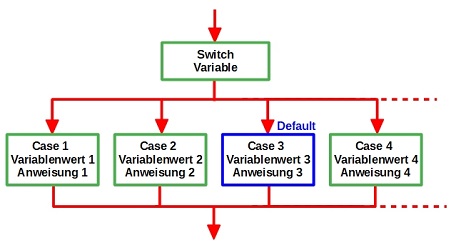 |
| Vor der Ausführung der unterschiedlichen Programmabschnitte wird zunächst eine Bedingung überprüft. Liefert diese den Wert "True", so wird Anweisung 1 ausgeführt. Wird die Bedingung nicht erfüllt (False), so wird Anweisung 2 ausgeführt. | Die mehrfache Verzweigung wird durch eine Variable gesteuert, die als Datentyp "Integer" zugeordnet hat. Je nach Variablenwert wird die zugehörige Anweisung ausgeführt. Liefert die Variable hingegen einen Wert, dem keine Anweisung zugeordnet wurde, so wird im diesem Fall das Standard-Programm, mit Default bezeichnet, ausgeführt. |
Grundsätzlich lassen sich Verzweigungen auch verschachteln, das heißt mehrere Verzweigungen werden ineinander gesetzt!

Bei der Ausführung von Programmen benötigt man immer wieder die Möglichkeit, Werte zu speichern um sie zu einem späteren Zeitpunkt wieder aufrufen zu können. Hierzu nutzen Programmiersprachen „Variablen“. Das sind „Platzhalter“ oder „Behälter“, die einerseits einen Variablenwert aufnehmen können und andererseits diesen gespeicherten Wert an das Programm zurückgeben können. Im Normalfall bezeichnet man Variablen mit einem charakteristischen, selbsterklärenden Namen, der vom Programmierer vergeben wird. Zur fehlerfreien Verwendung von Variablen empfiehlt es sich, Variablen vor ihrer ersten Benutzung zu initialisieren, das heißt man weißt ihnen eine definierten Startwert zu Beginn des Programms zu. Undefinierte und nicht initialisierte Variablen sind sehr häufig eine Quelle für schwer zu findende Fehler.
Beispiele:
 | Eine Variable „Speed“ speichert den Wert für die gewünschte Geschwindigkeit, mit der sich ein Fahrroboter bewegt. Diese kann sich zu jedem Zeitpunkt verändert und angepasst werden. |
 | Eine Variable „Antwort“ speichert die eingeloggte Antwort des Kandidaten bei einem Quiz mit vier möglichen Antworten um sie anschließend mit der richtigen Antwort abgleichen zu können. |
 | Eine Variable „Rekordhalter“ speichert den Spielernamen mit dem aktuell höchsten Punktestand bei einem Konsolenspiel und wertet ihn in einer Rangliste „High Score“ nach Spielende aus. |
 | Eine Variable „Lampe“ speichert, ob eine Kontroll-LED leuchtet(1) oder nicht (0). |
Grundlage für ein fehlerfreies Arbeiten mit Daten, Variablen und Konstanten sind der richtige Einsatz und die richtige Verwendung der unterschiedlichen Typen von Daten. Unabhängig vom Datentyp werden alle Daten in eine sogenannte Bitfolge (Folge aus Nullen und Einsen) konvertiert und gespeichert. Dabei entspricht eine Ziffer der Bitfolge genau einem Bit. 8 Bits fasst man zu einem Byte zusammen. Wie üblich werden anschließend die zugehörigen Vorsilben Kilo, Mega, Giga, usw. bei größeren Datenmengen verwendet (1 GByte = 1 000 MBytes = 1 000 000 KBytes = 1 000 000 000 Bytes = 8 000 000 000 Bits).
Alle Programmiersprachen bieten eine eigene Menge an vordefinierten Datentypen mit zugeordnetem Wertebereich und den darauf möglichen Operationen an. Grob lassen sich jedoch vier - weit verbreitete - Typen unterscheiden:
Boolean (auch Logiksignal oder Wahrheitswert)
Der boolesche Datentyp besitzt nur zwei verschiedene Werte und lässt sich am besten durch die Bezeichnungen an / aus, ja / nein, wahr / falsch oder 1 / 0 beschreiben. Ein boolescher Wert benötigt einen Speicherplatz von einem Bit und ist somit die kleinste Speichereinheit. Mit Hilfe der logischen Operationen AND, OR und NOT lassen sich Abfragen und Verzweigungen steuern.
Integer (auch Ganze Zahl)
Ein Integer ist eine Ganze Zahl, die auf einen von der Programmiersprache festgelegten Wertebereich eingegrenzt ist. Bei einem vorgesehenem Speicherplatz von 16 Bits pro Ganze Zahl lassen sich somit 216 = 65536 verschiedene Ganze Zahlen verwenden. Dazu verden die Ganzen Zahlen in Binärzahlen umgewandelt. Die Zahl 4231 wird also der Binärzahl 0001000010000111 zugeordnet. Operationen auf den ganzen Zahlen sind neben den mathematischen Grundrechenarten Addition, Subtraktion und Multiplikation auch Vergleiche (<, >, =). Bei der Division betrachtet man zumeist die Division mit Rest.
Float (auch Gleitkommazahl)
Floats sind sogenannte Gleitkommazahlen, die sich aus einem Vorzeichen, einer Mantisse und einem Exponenten zusammensetzen. Dabei gibt der Exponent die Kommastelle an. Soll bespielsweise die Zahl – 5236,4237 gespeichert werden, so wird als Vorzeichen ein Minus gespeichert, die Mantisse ist 52364237 und als Exponent wird die vier gespeichert, jeweils als Binärzahl. Alle Grundrechenarten (+, -, *, / ) sind als Operationen erlaubt, ebenso die Vergleiche (<, >, =)
String (auch Zeichenkette)
Zum Speichern von Zeichenketten und Texteinheiten verwendet man den Datentyp String. Je nach Computer werden diese Zeichen nach einem bestimmten Schlüsseln in eine Bitfolge kodiert und gespeichert. Ein bekannter solcher Zeichensatz ist der ASCII (7Bit) – Code, bei dem insgesamt 27 = 128 verschiedene Zeichen zur Verfügung stehen. Durch die Umwandlung / Konvertierung von Zeichenketten in Bitfolgen lassen sich als mögliche Operationen Vergleiche zwischen den Texteinheiten erstellen.
Sehr häufig enthalten Programnmiersprachen Befehle, die die einzelnen Datentypen ineinander überführen können. Beispielsweise kann die Gleitkommazahl 34,246 in eine Zeichenkette 34,246 konvertiert werden und anschließend mit anderen Texteinheiten verknüpft werden.
Beim Programmieren ist auf die richtige Verwendung der unterschiedlichen Datentypen mit den möglichen Operationen zu achten. Die Textvariable „Franz“ lässt sich logischerweise nicht durch die Ganze Zahl 4 teilen.

Programmieraufgaben zur Bewegung eines Roboters:
Programmieraufgabe 1: ParcoursProgrammieraufgaben zur Gestaltung des NXT-Displays:
Programmieraufgabe 6: Säulen auf dem Display

Aufgaben zur Bewegung eines Roboters:
Aufgabe 1: UmfangAufgaben zu den Datentypen:
Aufgabe 6: DatentypenAufgaben zu Flussdiagrammen:
Aufgabe 11: SymboleVermischte Aufgaben:
Aufgabe 16: Pentagramm