Das Binärsystem:

Klar! Wir haben zehn Finger und zehn Zehen. Deshalb ist es auch so geschickt, bis zehn zu zählen. Computer hingegen rechnen nicht mit dem vertrauten dezimalen Zahlensystem. Sie rechnen binär. Es gibt also nur zwei Ziffern: 0 und 1. Und dennoch lassen sich sowohl alle Zahlenwerte als auch alle Rechnungen in diesem Stellenwertsystem darstellen und durchführen. Der Grund für das Zweiersystem (Binärsystem oder auch Dualsystem) liegt in der Bauweise der Computer: Auch die verbauten elektronischen Schaltungen haben genau zwei elektrische Zustände, eben „Strom fließt“ bzw. 1 oder „Strom fließt nicht“ bzw. 0. Durch geschicktes Verschalten können so elektronische Rechenmaschinen, sprich Computer gebaut werden.

Zählen im Binärsystem

Grundsätzlich ist das Zählen im Zweiersystem dem Zählen im üblichen Zehnersystem sehr ähnlich. Um dies besser zu verstehen muss man sich jedoch noch einmal die Zählregeln im Dezimalsystem klar machen und anschließend auf das Zweiersystem übertragen:

Los geht es mit der kleinsten Ziffer, der 0. Anschließend zählt man die Ziffern hoch bis man an der größten Ziffer, der 9 angelangt ist(2, 3, 4, 5, 6, 7, 8, 9). Will man nun weiterzählen, so benötigt man eine weitere Stelle. Die 9 wird zunächst auf die 0 runtergesetzt und die nächst größere Stelle wird um 1 erhöht (10). Nun werden erneut die Ziffern bis 9 schrittweise erhöht (11, 12, 13, 14, 15, 16, 17, 18, 19). Immer wenn man bei der 9 angelangt ist wird diese auf 0 zurückgesetzt und die nächsthöhere Stelle um 1 erhöht (20). So lässt sich unter der Voraussetzung, dass man unendlich viele Stellen zur Verfügung hat, prinzipiell ungehindert weiterzählen.

Die Vorgehensweise beim Zählen im Binärsystem ist grundsätzlich die gleiche, allerdings hat man nun nicht 10, sondern nur 2 Ziffer:

Los geht es wieder mit der kleinsten Ziffer, der 0. Diese Ziffer wird nun erhöht auf 1. Da man nun bei der größten Ziffer im Zweiersystem angelangt ist, muss nun diese 1 wieder auf 0 zurückgesetzt werden. Allerdings darf man nicht vergessen, dass die nächst höhere Stelle um 1 erhöht werden muss (10). Es gilt also: Immer wenn man bei der 1 angelangt ist wird diese auf 0 zurückgesetzt und die nächsthöhere Stelle um 1 erhöht. Wie im Zehnersystem lässt sich so bei unendlich vielen verfügbaren Stellen unbegrenzt weiterzählen.

Die Tabelle zeigt die ersten 17 Zahlen im Zehner-, bzw Zweiersystem:

Dezimalsystem	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Binärsystem	0	1	10	11	100	101	110	111	1000	1001	1010	1011	1100	1101	1110	1111	10000	10001

Schreibweise

Will man nun gezielt angeben, in welchen Stellenwertsystem die Zahl dargestellt ist, so wird die Basis des Stellenwertsystems am Ende der Ziffern als kleiner Index festgesetzt. Die natürliche Zahl 23 im Zehnersystem entspricht dabei der 10111 im Zweiersystem:

23₁₀ = 10111₂

Die übliche Darstellung von Zahlen ist bereits selber schon eine besondere Schreibweise. Hinter einer Ziffernfolge steht eigentlich eine Rechnung mit Potenzen der Basis im jeweiligen System. Dies verdeutlicht das Beispiel:

58369₁₀ = 5 ⋅ 10000₁₀ + 8 ⋅ 1000₁₀ + 3 ⋅ 100₁₀ + 6 ⋅ 10₁₀ + 9 ⋅ 1₁₀ = 5 ⋅ 10⁴ + 8 ⋅ 10³ + 3 ⋅ 10² + 6 ⋅ 10¹ + 9 ⋅ 10⁰

abcde₁₀ = a ⋅ 10000₁₀ + b ⋅ 1000₁₀ + c ⋅ 100₁₀ + d ⋅ 10₁₀ + e ⋅ 1₁₀ = a ⋅ 10⁴ + b ⋅ 10³ + c ⋅ 10² + d ⋅ 10¹ + e ⋅ 10⁰

Ebenso lässt sich eine Zahl im Binärsystem mit Hilfe von Potenzen der Basis 2 darstellen:

10111₂ = 1 ⋅ 10000₂ + 0 ⋅ 1000₂ + 1 ⋅ 100₂ + 1 ⋅ 10₂ + 1 ⋅ 1₂ = 1 ⋅ 2⁴ + 0 ⋅ 2³ + 1 ⋅ 2² + 1 ⋅ 2¹ + 1 ⋅ 2⁰

abcde₂ = a ⋅ 10000₂ + b ⋅ 1000₂ + c ⋅ 100₂ + d ⋅ 10₂ + e ⋅ 1₂ = a ⋅ 2⁴ + b ⋅ 2³ + c ⋅ 2² + d ⋅ 2¹ + e ⋅ 2⁰

Im Prinzip läuft im Binärsystem also alles genau „gleich“ ab. Basis ist hier allerdings die 2; und demzufolge gibt es auch nur die zwei Ziffern 0 und 1.

Umwandeln von Binärzahlen in Dezimalzahlen

Eine Tabelle eignet sich am besten, um das Verfahren beim Umwandeln von Binärzahlen in das Dezimalsystem übersichtlich darzustellen. In der obersten Zeile stehen dabei die Zweierpotenzen von rechts nach links. Nach dem Ausfüllen einer Zeile addiert man anschließend genau die Zweierpotenzen, bei denen in der jeweiligen Spalte eine 1 steht.

Umwandeln von Dezimalzahlen in Binärzahlen

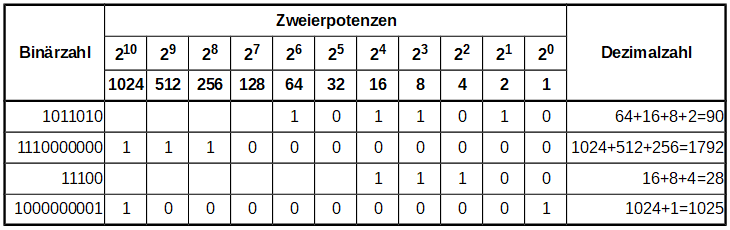
Prinzipiell kann man beim Umwandeln von Dezimalzahlen ins Zweiersystem genauso wie oben vorgehen. Ziel ist es dabei, die gegebene Dezimalzahl als Summe einzelner Zweierpotenzen darzustellen.

In einem ersten Schritt sucht man dabei die größte Zweierpotenz, die kleiner als die gegebene Dezimalzahl ist. Diese Zweierpotenz ist demnach der größte Summand in der Darstellung der Zahl als Summe und wird genau 1-mal benötigt.

Anschließend subtrahiert man diese Zweierpotenz von der vorgebenen Zahl und untersucht, ob die nächstkleinere Zweierpotenz in die neue kleinere Zahl passt, die sich aus der Subtraktion ergeben hat.

Falls ja, dann wird die Zweierpotenz wiederum 1-mal in der Summendarstellung benötigt. Sie wird erneut abgezogen und die sich daraus ergebende Differenz weiter untersucht.

Falls nein, dann wird diese Zweierpotenz genau 0-mal in der Summendarstellung benötigt. Eine Differenz muss nun nicht gebildet werden und die nächst kleinere Zweierpotenz wird untersucht.

Diese Schritte wiederholen sich bis die kleinste Zweierpotenz 2⁰ = 1 untersucht ist.

Am besten versteht man das Verfahren wenn man das Beispiel mit der Zahl 745 betrachtet:

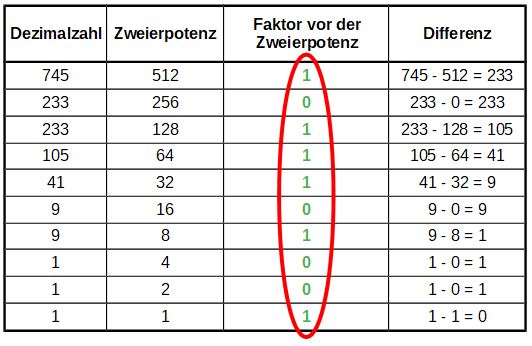
Ergebnis:

An den fett gedruckten Faktoren vor den Zweierpotenzen lassen sich nun einerseits die Summendarstellung der Dezimalzahl als auch die gesuchte Binärzahl selber ablesen.

745 = 1⋅512 + 0⋅256 + 1⋅128 + 1⋅64 + 1⋅32 + 0⋅16 + 1⋅8   + 0⋅4  + 0⋅2 +  1⋅1 

745 = 1⋅2⁹    + 0⋅2⁸   + 1⋅2⁷   + 1⋅2⁶ + 1⋅2⁵ + 0⋅2⁴ + 1⋅2³ + 0⋅2² + 0⋅2¹ + 1⋅2⁰

745₁₀ =1011101001₂

Weiteres Verfahren über die Division mit Rest:

Zur Umwandlung von Dezimalzahlen in Binärzahlen gibt es noch ein weiteres Verfahren, das sich auch leicht mit einem Computer programmieren lässt. Dabei spielt die Division mit Rest eine große Rolle.

Schrittweise werden von einer gegebenen Zahl die Reste bei der Division mit 2 bestimmt. Diese ergeben dann die Ziffern der zugehörigen Binärzahl wie das Beispiel mit der Zahl 35 unten zeigt:

Ergebnis:

Das Ergebnis kann nun leicht einerseits an den Resten oben oder andererseits an der sich ergebenden Summendarstellung abgelesen werden:

35 = 2⁵ + 2¹ + 2⁰

35 = 1⋅2⁵ + 0⋅2⁴ + 0⋅2³ + 0⋅2² + 1⋅2¹ + 1⋅2⁰

35₁₀ =100011₂

Rechnen mit Binärzahlen

Addition

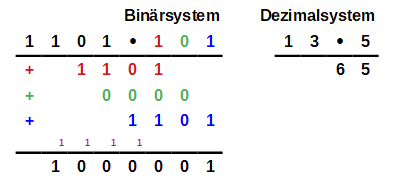
Im Prinzip funktioniert das schriftliche Addieren und Subtrahieren mit Binärzahlen genauso wie das schriftliche Addieren und Subtrahieren im Zehnersystem. Allerdings müssen die Rechenregeln konsequent in das Zweiersystem übertragen werden. Da es nur 2 Ziffern gibt erfolgt beispielsweise der Übertrag auf die nächst höhere Stelle schon bei einer Addition von zwei Einsen ( 1 + 1 = 10 ).

Insbesondere bei der Addition mehrerer Binärzahlen kann es auch vorkommen, dass der Übertrag nicht nur auf die nächst höhere Stelle erfolgt, sondern sogar eine Stelle weiter berücksichtigt werden muss. Dies erkennt man gut an den Beispielen: Bei der Addition der letzten Stelle erhält man im Binärsystem 1 + 1 + 1 + 1 = 100. Es wird als eine Null auf die nächst höhere Stelle übertragen und eine Eins auf die übernächste Stelle (roter Übertrag). Ebenso muss auch bei der folgenden Addition der Übertrag auf die beiden nächsten Stellen beachtet werden (grüner Übertrag).

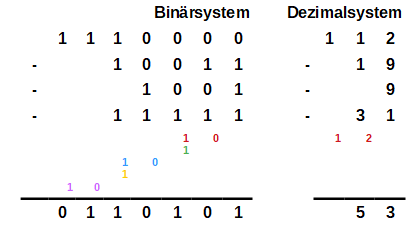
Subtraktion

Auch das bekannte Verfahren beim schriftlichen Subtrahieren im Dezimalsystem lässt sich völlig analog auf das Zweiersystem übertragen. Wie im Zehnersystem muss man auch im Zweiersystem bei Bedarf die Zahl, von der man etwas abzieht, erweitern. Dieses Erweitern wird durch den anschließenden Übertrag ausgeglichen. Durch das kleinschrittige Vergleichen der beiden Beispiele unten erkennt man das Prinzip der schriftlichen Subtraktion.

    

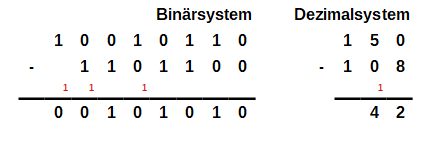
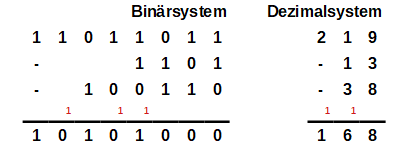
Beim Erweitern und Übertragen muss man jedoch aufpassen: Wie bei der Addition kann es vorkommen, dass man die Zahl, von der man abziehen möchte, um mehrere Stellen erweitern muss. Dementsprechend muss dann auch der Übertrag bei mehreren Stellen berücksichtigt werden. Bei der unteren Subtraktion gehören immer die Übertrage gleicher Farbe zusammen:

Multiplikation

Auch bei der Multiplikation zweier Binärzahlen muss man diese nicht zuvor in Dezimalzahlen umwandeln und dann im Zehnersystem rechnen. Auch die schriftliche Multiplikation und die schriftliche Division lassen sich bei genauem Anwenden der Rechenregeln im Zweiersystem direkt durchführen. Zu beachten ist lediglich, dass ( 0 ⋅ 0 ) , ( 0 ⋅ 1 ) und ( 1 ⋅ 0 ) jeweils 0 ergibt. Nur die Multiplikation ( 1 ⋅ 1 ) ergibt eine 1. Bei Binärzahlen mit mehreren Ziffern müssen die Einzelprodukte natürlich wie üblich nach den Rechenregeln der Addition aufsummiert werden.

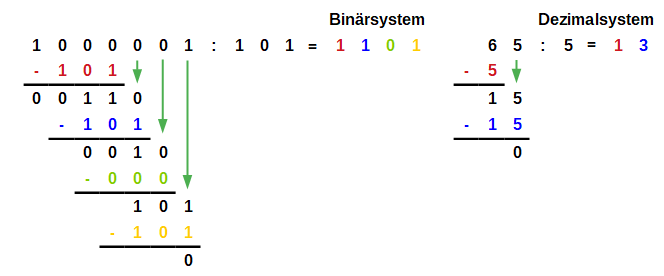
Division

Binäre Divisionsaufgaben können ebenso mit dem gleichen Verfahren wie bei der schriftlichen Division im Zehnersystem gelöst werden. Das untere Beispiel verdeutlicht das Rechenverfahren, das jedoch schon ein wenig Übung im Umgang mit Binärzahlen benötigt.

Zahlen im Binärsystem können schnell eine unübersichtliche Länge haben, die nur noch schwer handzuhaben sind. Deshalb wird vor allem häufig das Hexadezimalsystem verwendet, das im folgenden kurz vorgestellt wird.

Das Hexadezimalsystem

Der Begriff „Hexadezimalsystem“ ist ein griechisch-lateinisches Mischwort, das sich aus dem griechischen Wort „hexa“ für „sechs“ und dem lateinischen Wort „decem“ für „zehn“ zusammensetzt. Demzufolge hat dieses Stellewertsystem also 16 Ziffern: die üblichen Ziffern von 0 bis 9 und zusätzlich noch die sechs Buchstaben von A bis F. Die Tabelle zeigt die ersten 17 Zahlen im Zehner-, bzw Hexadezimalsystem:

Dezimalsystem	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Hexadezimalsystem	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10	11

In der Datenverarbeitung / Informatik haben sich zur Verwaltung von Daten (Textdaten, Bilddaten, etc. ) Ketten von achstelligen Binärzahlen durchgesetzt. Dabei entspricht jeder achtstelligen Binärzahl beispielsweise genau ein Textzeichen oder ein Farbwert (genau 1 Byte). Anstelle der achtstelligen Binärzahl greift man für die übersichtliche und komfortable Darstellung auf die zugehörige Hexadezimalzahl zurück. Hexadezimalzahlen und Binärzahlen lassen sich sehr leicht ineinander umwandeln, da eine Ziffer im Hexadezimalsystem genau einem Viererblock im Binärsystem entspricht.

Durch die konsequente Anwenung der Rechenregeln lassen sich Hexadezimalzahlen ins Dezimalsystem umwandeln, dabei spielen wiederum Potenzen zur Basis 16 eine Hauptrolle:

DAFA₁₆ = D ⋅ 1000₁₆ + A ⋅ 100₁₆ + F ⋅ 10₁₆ + A ⋅ 1₁₆ = 13 ⋅ 16³ + 10 ⋅ 16² + 15 ⋅ 16¹ + 10 ⋅ 16⁰  = 53248 + 2560 + 240 + 10 = 56058₁₀

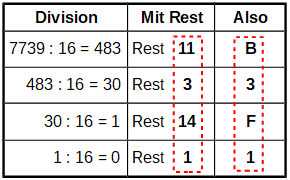
Umgekehrt kann man mit Hilfe der Division mit Rest Dezimalzahlen ins Hexadezimalsystem überführen. Der Teiler ist jedoch in diesem Fall 16.

Weitere Stellenwertsysteme

Neben den oben dargestellten Stellenwertsysteme sind im Bereich der Datenverarbeitung auch noch das Oktalsystem (Achtersystem mit den Ziffern von 0 bis 7) und das Duodezimalsystem (Zwölfersystem mit den Ziffern von 0 bis B) üblich. Aus mathematischer Sicht ist natürlich jedes Stellenwertsystem mit einer natürlichen Zahl als Basis denkbar.

Schriftliches Rechnen mit Binärzahlen:

Gegeben sind die folgenden fünf Binärzahlen:

Aufgabe:

a)	Untersuche in Kleingruppen die vier Grundrechenarten im Binärsystem: Addiere, subtrahiere, multipliziere und dividiere hierzu schriftlich jeweils verschiedene der oben gegebenen Binärzahlen und überprüfe deine Rechnungen indem du die Binärzahlen ins Zehnersystem umwandelst und die Rechnungen dann durchführst!
b)	Erstelle einen übersichtlichen und klar strukturierten Heftaufschrieb mit Beispielen und Regeln zu einer Grundrechenart deiner Wahl. Diese Heftaufschriebe zu allen Grundrechenarten können anschließend zu einem kleinen Regelheft zusammengefasst und vervielfältigt werden.

Addition:

Subtraktion:

Multiplikation:

Division:

Zaubertrick:

Ein Zauberer findet aus einem gut gemischten Kartenstapel das heutige Datum. Dazu muss er mehrmals die Farbe bestimmter Karten erraten. Hat er richtig geraten, so erhält der Zauberer einen Punkt, beim falschen Raten natürlich keinen Punkt. Die Folge von 0 und 1 ist die Binärdarstellung des gesuchten Datums.

Zunächst einmal muss ein Kartenstapel etwas präpariert werden. Die Karten müssen abwechselnd "rot" oder "schwarz" sein, das Kartenbild hingegen spielt dabei keine Rolle. Wird der Stapel anschließend etwas "unsauber" offen auf dem Tisch ausgebreitet, so haben die Zuschauer das Gefühl, dass die Karten unsortiert nebeneinander liegen.

Nun wird der Stapel zusammengeschoben und umgedreht. Zuschauer dürfen nun mehrmals vom verdeckten Stapel "Abheben". Dadurch wird die Sortierung in rote und schwarze Karten nicht durcheinandergebracht. Für einen größeren Überraschungseffekt ist also ein weiteres Mischen notwendig: Dazu werden die Karten verdeckt von oben einzeln auf einen weiteren Stapel heruntergezählt, bis ein Zuschauer "Stopp" sagt. Geschickt ist es, wenn etwa zwei gleich große Stapel entstehen.

Zur Kontrolle sollten nun bei beiden Stapeln unten Karten mit verschiedenen Farben liegen.

Jetzt können die beiden Stapel durch übliches Mischen zusammengeführt werden. Die Daumen heben dabei leicht die beiden Stapel an der Seite an und lassen anschließend die Karten zufällig sowohl vom rechten als auch vom der linken Seite ineinanderfallen. Anschließend können die Stapel dann zusammengeschoben werden. Mehrmaliges Mischen in dieser Art bringt das Kartenspiel zumindest scheinbar "perfekt" durcheinander. Zusätzliches "Abheben" kann natürlich den Anschein, perfekt gemischter Karten verstärken.

All das Mischen hat nichts genutzt: Die Karten liegen immernoch abwechselnd "rot" oder "schwarz".

Nun geht es an das Erraten der Kartenfarbe. Dazu wird von oben eine Karte an den Zuschauer gegeben, die nächste Karte behält der Zauberer. Das geht natürlich auch genau umgekehrt. Beide können nun ihre, aber nur ihre Karte anschauen. Ist die Karte des Zauberers "rot", so weiß er automatisch und garantiert, dass die Zuschauerkarte "schwarz" sein muss, oder eben genau andersherum. Er muss also nur noch entscheiden, ob er einen Treffer erzielen muss, um eine 1 zu erzeugen, oder ob er sich irren soll, um eine 0 zu realisieren. Ein Assistent notiert das Rateergebnis. Nun werden diese beiden Karten auf die Seite gelegt. Ein weiterer Zuschauer erhält nun wieder eine Karte eines "Pärchens", der Zauberer die anderer. Hier ist schauspielerisches Geschick gefragt. Der Zauberer muss immer wieder die Reihenfolge wechseln, wer die erste Karte des "Pärchens" erhält. So kann vermieden werden, dass der Zuschauer beispielsweise immer eine rote Karte erhält. Sicherlich werden sich die Zuschauer auch fragen, warum sich der Zauberer denn so oft mit seinem Erraten der Kartenfarbe vertut. Die große Überraschung erfolgt dann, wenn die scheinbar zufällige Folge aus 0 und 1 tatsächlich einen Sinn ergibt.

Aufgaben:

Aufgaben mit Binärzahlen:

Aufgabe 1: Umwandlungen 1
Aufgabe 2: Binäruhr
Aufgabe 3: Besonderheiten
Aufgabe 4: Umwandlung mit Algorithmus
Aufgabe 5: Rechnen mit Binärzahlen

Vermischte Aufgaben:

Aufgabe 6: Umwandlungen 2
Aufgabe 7: Basketball
Aufgabe 8: Weitere Stellenwertsysteme
Aufgabe 9: Kontoauszug
Aufgabe 10: Restaurant
Aufgabe 11: Wahlen