
 |
Optik |
|
Zweifelsohne ist das Auge das wichtigste menschliche Sinnesorgan. Es hilft uns bei der Orientierung, eröffnet uns wundervolle Ein- und Ausblicke und warnt uns vor Gefahren Zum Sehen benötigen wir aber Licht. Aus diesem Grund ist die Erforschung des Lichts in der Optik Grundlage für ein besseres Verständnisses des Sehvorgangs. Licht transportiert aber auch Informationen und ist deshalb von hohem wissenschaftlichen und technischen Interesse. So helfen Teleskope beispielsweise über das eintreffende Licht aus dem Weltall Rückschlüsse auf die Geheimnisse ferner Sterne zu trefffen. Lichtwellenleiter übetragen Internetseiten und Emails in kürzester Zeit über Kontinente hinweg. Mikroskopen könnten kleinste Strukturen auflösen und sichtbar machen. Sogar über die kleinsten Bausteine der Materie, den Atomen kann Licht uns bei geschickter Analyse Informationen geben.
BrechungLicht breitet sich geradlinig aus. Aus diesem Grund spricht man gerne auch von Lichtstrahlen. Beim Übergang eines Lichtstrahls von einem Medium (etwa Luft) in ein anderes (etwa Wasser) teilt sich dieser Lichtstrahl auf. Ein Teil des Lichts wird an der Grenzfläche der beiden Medien nach dem Reflexionsgesetz (Einfallswinkel ist gleich Reflexionswinkel, gemessen zum Lot) zurückgeworfen, ein Teil des Lichts breitet sich jedoch auch im anderen Medium aus. Allerdings scheint dieser Lichtstrahl beim Übergang vom einen Medium in das andere einen „Knick“ zu bekommen. Er ändert seine Ausbreitungsrichtung, verläuft aber auch im zweiten Medium wieder geradlinig. Sowohl der einfallende Lichtstrahl, der gebrochene Lichtstrahl sowie der reflektierte Lichtstrahl liegen in einer Ebene, der sogenannten Einfallsebene. Dieses Phänomen nennt man Brechung.
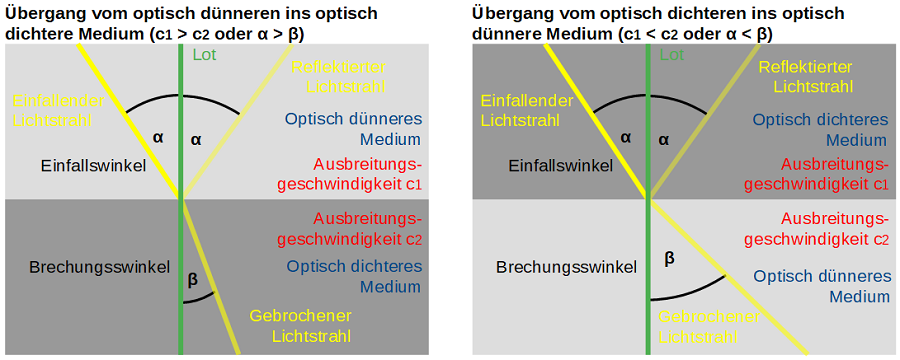
Das „Abknicken“ des Lichtstrahls an der Grenzfläche zwischen zwei Medien lässt sich auf die unterschiedlichen Ausbreitungsgeschwindigkeiten in den jeweiligen Medien zurückführen. Die Ursache für die Lichtbrechung ist also, dass sich Licht in unterschiedlichen Medien unterschiedlich schnell ausbreitet. Diese unterschiedliche Ausbreitungsgeschwindigkeit hängt dabei von der Struktur, der Beschaffenheit und des Aufbaus des Medium ab. Diese unterschiedlichen Materialeigenschaftem fasst man im Begriff der „optischen Dichte“ zusammen: in optisch dünneren Medien ist die Geschwindigkeit des Lichts größer, in optisch dichteren Medien hingegen deutlich geringer. Beim Übergang von einem optisch dünneren Medium in ein optisch dichteres Medium wird der Lichtstrahl also zum Lot hin gebrochen (Einfallswinkel ist größer als Brechungswinkel). Umgekehrt gilt: Beim Übergang von einem optisch dichteren Medium in ein optisch dichteres Medium wird der Lichtstrahl vom Lot weg gebrochen (Einfallswinkel ist kleiner als Brechungswinkel).
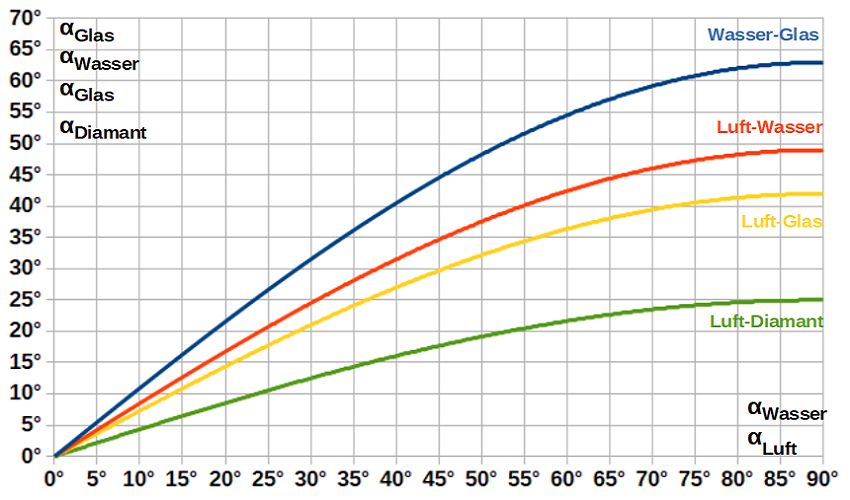
Die genaue Zuordnung zwischen dem Einfallswinkel und dem Brechungswinkel muss in Einzelfall bestimmt werden. Das Diagramm zeigt vier Beispiele: Zu jedem Einfallswinkel kann der zugehörige Brechungswinkel abgelesen werden.
Um die optische Brechung etwas genauer zu verstehen hilft das Prinzip von Fermat (berühmter Naturwissenschaftler und Mathematiker, 1601 bis 1665). Er untersuchte die benötigte Zeit, die Licht von einem Punkt A zu einem Punkt B benötigt und stellte daraufhin seinen Grundsatz auf. Vereinfacht lautet das sogenannte Fermatsche Prinzip (oder auch Minimalprinzip):
Von allen denkbaren möglichen Lichtwegen zwischen A und B, nimmt das Licht den Weg, der die kürzeste Zeit benötigt!
Offentsichtlich ist der zeitlich kürzeste Weg zwischen zwei Punkten A und B ohne Übergange in verschiedene Medien der geradlinige Weg. Dieser Weg ist sowohl der kürzeste als auch der zeitlich kürzeste Weg. Bei der geradlinigen Lichtausbreitung in einem bestimmten homogenen Medium ist also das Fermatsche Prinzip erfüllt. Auch bei der Reflexion an einem Spiegel ist der kürzeste Weg auch der zeitlich kürzeste Weg – genau der Weg, bei dem das Reflexionsgestz erfüllt ist. Wie aber kann man das Fermatsche Prinzip bei Übergängen von einem Medium in ein anderes mit unterschiedlicher Ausbreitungsgeschwindigkeit verstehen? Dazu hilft folgendes Beispiel:
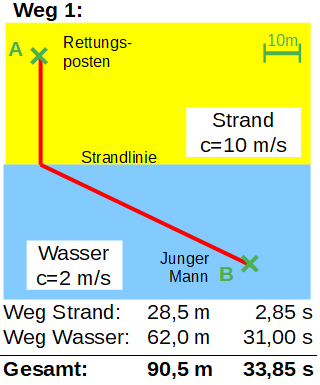
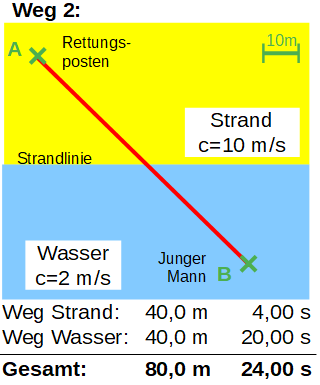
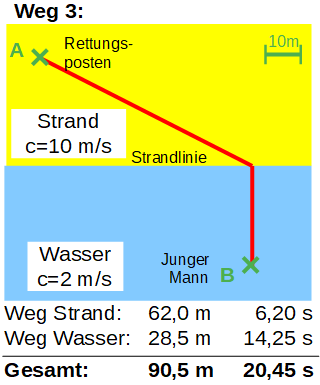
An einem langen Sandstrand befindet sich ein Rettungsposten, um den Küstenabschnitt zu überwachen. Mit einem Fernglas entdeckt ein Rettungsschwimmer, dass ein junger Mann schon weit von der Strandlinie entfernt in Not gerät und wohl nicht mehr aus eigener Kraft ans Land schwimmen kann. Ein Einsatz ist also dringend erforderlich. Mit der Rettungsboje in der Hand rennt der Rettungsschwimmer also über den Strand bis er das Wasser erreicht (Strandlinie) und schwimmt dann so schnell wie möglich zu dem jungen Mann. Die Abbildungen zeigen die genaue Lage der Situation. Welchen Weg aber muss der Rettungsschwimmer nun einschlagen? Rennt er vom Posten zuerst geradlinig zur Strandlinie und schwimmt dann zum Opfer? Oder rennt er zuerst möglichst lange über den Strand um dann eine möglichst kurze Schwimmstrecke vor sich zu haben? Klar ist: Am Strand kann der Rettungsschwimmer natürlich deutlich schneller rennen (vereinfacht ca. 10 m/s) als er im Wasser schwimmen könnte (vereinfacht ca. 2 m/s). Die Frage ist also, welcher Weg vom Rettungsposten zum jungen Mann ist der zeitlich schnellste Weg?
 |
 |
 |
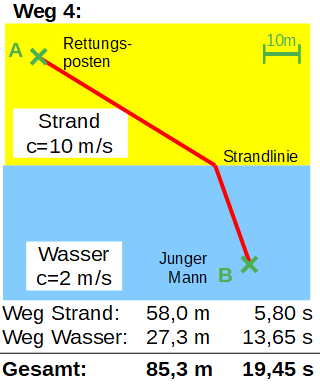 |
Im dargestellten Beispiel erkennt man, dass der Weg 4 der zeitlich kürzeste Weg ist, aber nicht der kürzeste, das ist nämlich der Weg 2 – die direkte Verbindung! Aufgrund der unterschiedlichen Geschwindigkeiten ergibt sich also ein Weg mit einem „Knick“ an der Strandlinie als kürzeste Verbindung zwischen dem Rettungsposten bei A und dem zu rettenden jungen Mann bei B.
Geht ein Lichtstrahl von einem Punkt A im Medium 1 mit einer Ausbreitungsgeschwindigkeit c1 aus und soll einem Punkt B in einem anderen Medium mit unterschiedlicher Ausbreitungsgeschwindigkeit c2 schnellst möglich erreichen, so nimmt das Licht nach dem Fermatschen Prinzip von allen möglichen Wegen genau den Weg, für den es die kürzeste Zeit benötigt. Wie stark der „Knick“ an der Grenzfläche zwischen den beiden Medien ist wird vom Verhältnis der beiden unterschiedlichen Ausbreitungsgeschwindigkeiten bestimmt. Diesen Quotienten bezeichnet man auch als Brechungsindex n. Also auch beim Übergang von Licht in unterschiedliche transparente Medien ist das Fermatsche Prinzip erfüllt.
TotalreflexionEin besonderes Phänomen tritt auf, wenn ein Lichtstrahl von einem optisch dichteren Medium in ein optisch dünneres Medium übergeht. Dazu betrachtet man am besten folgenden Spezialfall: Bei einem bestimmten Einfallswinkel αGrenz im optisch dichteren Medium wäre nach obigem Diagramm der zugehörige Brechungswinkel genau 90°. Das würde aber bedeuten, dass der gebrochene Lichtstrahl parallel zur Grenzfläche verlaufen würde, ein schwer zu realisierender Grenzfall. Bei noch größeren Einfallswinkel α verschwindet der gebrochene Lichtstrahl im optisch dünneren Medium. Nur mehr der reflektierte Lichtstrahl ist zu erkennen. Kein Licht dringt mehr in das optisch dünnere Medium ein, der Lichtstrahl wird vollständig reflektiert. Totalreflexion nennt man dieses Phänomen.
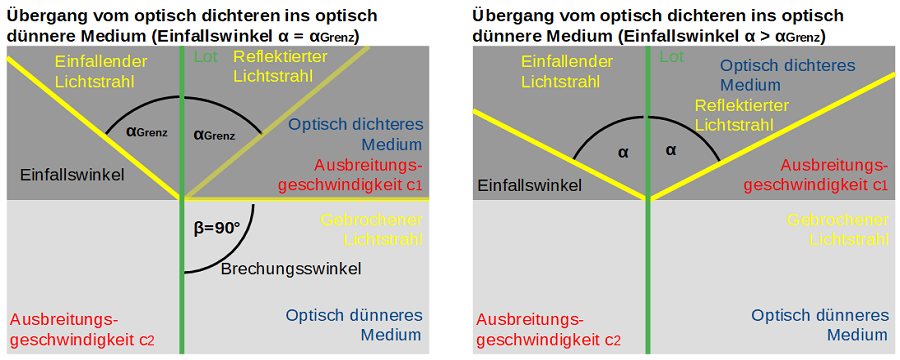
Die Größe des Grenzwinkels αGrenz hängt von wiederum von den Ausbreitungsgeschwindigkeiten der beteiligiten Medien ab.
LinsenMit Hilfe von optischen Linsen versucht man nun, Lichtstrahlen gezielt durch Brechungen an Grenzflächen zwischen Luft und Glas umzuleiten. Je nach Linsenform können so Lichtstrahlen gebündelt, fokusiert oder zerstreut werden. Im Normalfall sind die Oberflächen der Linsen gleichmäßig gewölbt. Man unterscheidet folgende spezielle Linsenformen:
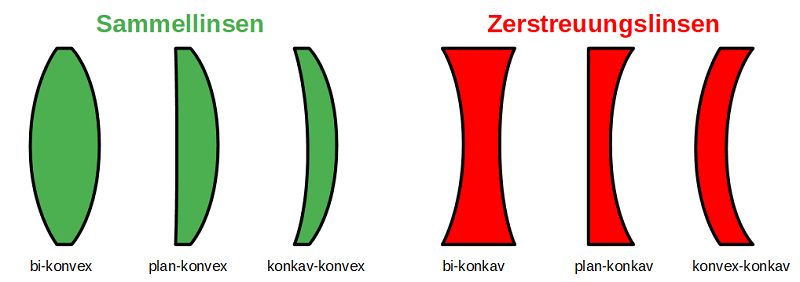
Strahlengang bei Sammellinsen
Sammellinsen sind genau so geformt, dass sich parallel – einfallendes Licht nach den zwei Brechungen beim Übergang Luft – Glas und beim Übergang Glas – Luft gerade in einem Punkt, dem sogenannten Brennpunkt F sammelt. Zur Vereinfachung fasst man die zwei Brechungen an den beiden Grenzflächen zu einer Brechung an der Linsenebene zusammen. Die genau Lage des Brennpunkts ergibt sich durch die Brennweite f. Das ist der Abstand zwischen der Linsenebene und dem Brennpunkt.
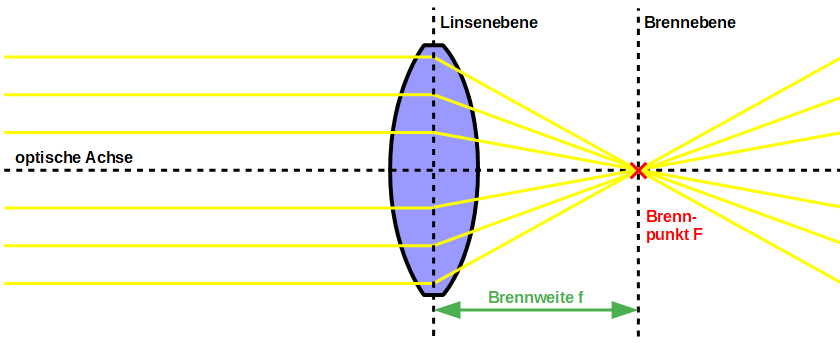
Strahlengang bei Zerstreuungslinsen
Zerstreuungslinsen hingegen sind genau so geformt, dass sich parallel – einfallendes Licht nach den zwei Brechungen beim Übergang Luft – Glas und beim Übergang Glas – Luft gerade so zerstreut, als wäre es ursprünglich aus einem Punkt, dem sogenannten Brennpunkt F gekommen. Zur Vereinfachung fasst man wieder die zwei Brechungen an den beiden Grenzflächen zu einer Brechung an der Linsenebene zusammen. Mit Hilfe der Brennweite f kann man wiederum die genau Lage des Brennpunkts bestimmen.
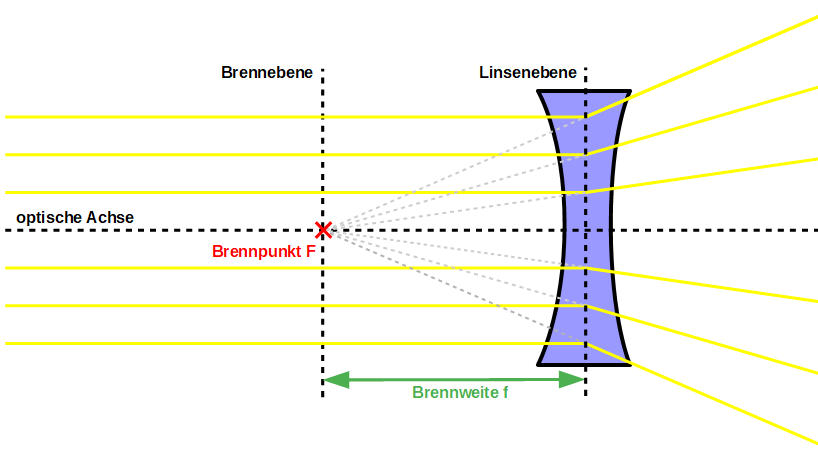
Abbildungen mit Linsen
Mit Hilfe von Sammellinsen können Gegenstände abgebildet werden. Ist der Abstand des Gegenstandes g zur Linsenebene größer als die Brennweite f, so entsteht auf der anderen Seite der Linsenebene ein reelles Bild, das entweder mit einem Schirm aufgefangen oder mit einer Kamera abfotografiert werden kann. Zur genauen Konstruktion des Bildes benötigt man ausgezeichnete Lichtstrahlen, sogennannte Haupt- oder Konstruktionsstrahlen. Diese drei Strahlen – achsenparaller Strahl, Brennpunktstrahl und Mittelpunktstrahl – sind Hilfsmittel zur Bestimmung der Bildpunkte, sie entsprechen jedoch nicht dem Lichtweg durch die Linse, der das Bild entstehen lässt. Vereinfacht gilt:
• Ein achsenparalleler Lichtstrahl (parallel zur optischen Achse) wird an der Linsenebene zu einem Brennpunktstrahl (in der Abbildung „rot“).
• Ein Brennpunktstrahl wird an der Linsenebene zu einem achsenparallelen Strahl (in der Abbildung „grün“).
• Ein Mittelpunktstrahl behält nach der Linsenebene seine Richtung bei (in der Abbildung „blau“).
Mit diesen Regeln lässt sich der Strahlengang an einer Sammellinse konstruieren:
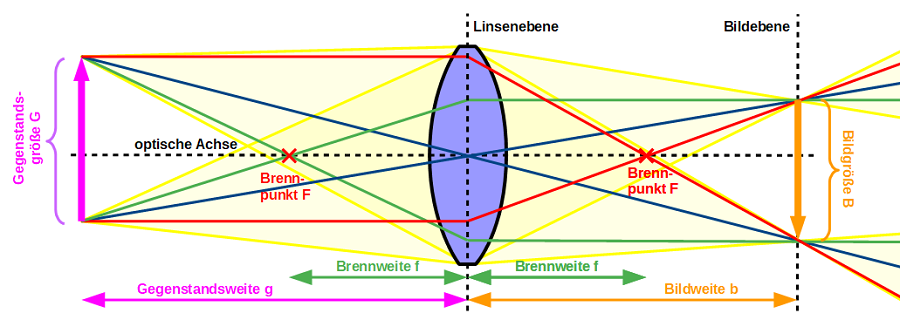
Die Konstruktionsstrahlen bestimmen die Lage des scharfen Bildes, denn sie schneiden sich nach der Linsenebene in einem Punkt. Der Verlauf der Lichtstrahlen selber wird durch die Größe der Linse bestimmt. Deutlich zu erkennen ist, dass die Bildgröße B kleiner als die Gegenstandsgröße G ist. Ebenso ist das Bild auf dem Kopf und seitenverkehrt.
Abbildungsgleichung
Über die Strahlensätze der Mathematik kann man erkennen, dass das Verhaltnis von Gegenstandsgröße G zu Bildgröße B genau so groß ist wie das Verhältnis der Gegenstandsweite g zur Bildweite b. Diesen Zusammenhang nennt man auch Abbildungsgleichung. Sie lautet:
Kennt man also drei der Größen, so lässt sich die vierte leicht berechnen.
Linsengleichung
Aber auch die drei Weiten – Brennweite f, Gegenstandsweit g und Bildweite b – stehen in einem Zusammenhang. Wieder lässt sich über mathematische Strahlensätze die sogenannte Linsengleichung herleiten. Sie lautet:
Kennt man etwa die Brennweite f der Linse und ist bekannt, wie groß der Abstand zwischen Linse und Gegenstand ist (Gegenstandsweite g), so lässt sich berechnen, in welcher Entfernung das Bild entsteht (Bildweite b).
Solange die Gegenstandsweite g größer als die Brennweite f ist, gilt: Nähert sich der Gegenstand der Linse, so entfernt sich das Bild von der Linse. Soll das Bild kleiner als der Gegenstand sein, so muss die Brennweite größer als die doppelte Brennweite sein ( g > 2f ). In diesem Fall entsteht das Bild zwischen der einfachen Brennweite und der doppelten Brennweite ( f < b < 2f ). Ein vergrößertes Bild erhält man, wenn die Gegenstandsweite zwischen der einfachen und der doppelten Brennweite ist ( f < g < 2f ). Nun entsteht das Bild bei einer Brennweite, die größer als die doppelte Brennweite ist ( b > 2f ). Gegenstand und Bild sind genau dann gleich groß wenn sowohl Gegenstandsweite g als auch Bildweite b genau der doppelten Brennweite f entsprechen.
Optische GeräteZahlreiche Konstruktionen und Erfindungen machen sich die oben beschriebenen optischen Regeln und Gesetze zu Nutze, meistens um kleine Strukturen oder weit entfernte Gegenstände vergrößert darzustellen. Aber auch die Biologie kennt die Gesetze der Lichtbrechung. Das Auge bildet zusammen mit der Netzhaut ein Linsensystem, das sogar in der Lage ist, die Brennweite f der Augenlinse durch Veränderung der Linsenwölbung zu variieren.
Bewegt man die Hand auf das Auge zu, so erscheint sie immer größer und kleinere Strukturen auf der Handoberfläche werden deutlicher. Allerdings sind dieser Annäherung Grenzen gesetzt. Mit geringerem Abstand des Gegenstandes zum Auge wird das Scharfstellen zunehmend anstrengender bis es ab ca. 10 cm Entfernung gar nicht mehr möglich ist. Will man noch kleiner Strukturen auflösen, so benötigt man zur Vergrößerung „optische Geräte“. Das einfachste dieser Art ist die Lupe.
Lupe
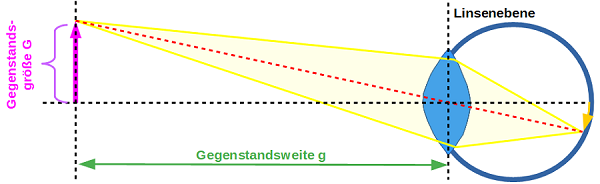
Eine Lupe ist nichts anderes als eine Sammellinse, die direkt vor das Auge gehalten wird. Dabei ist zu beachten, dass sich der zu betrachtende Gegenstand genau im Abstand der Brennweite f – also in der Brennebene – vor der Linse befindet. Dadurch sind die Lichstrahlen, die von einem Punkt des Gegenstands loslaufen nach der Linse gegeneinander parallel. Die Richtung der parallelen Lichtstrahlen ergibt sich durch den Hauptstrahl. Die Augenlinse fokusiert diese parallelen Lichtstrahlen in einem Punkt auf der Netzhaut, ein vergrößertes Bild des Gegenstandes entsteht.
Astronomisches Fernrohr
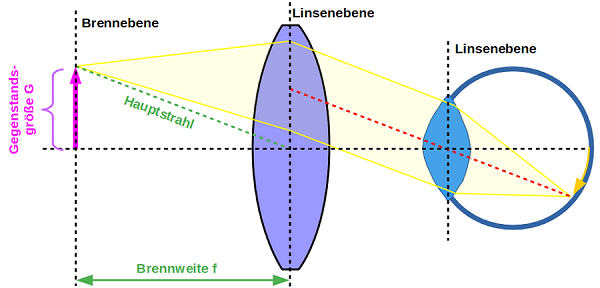
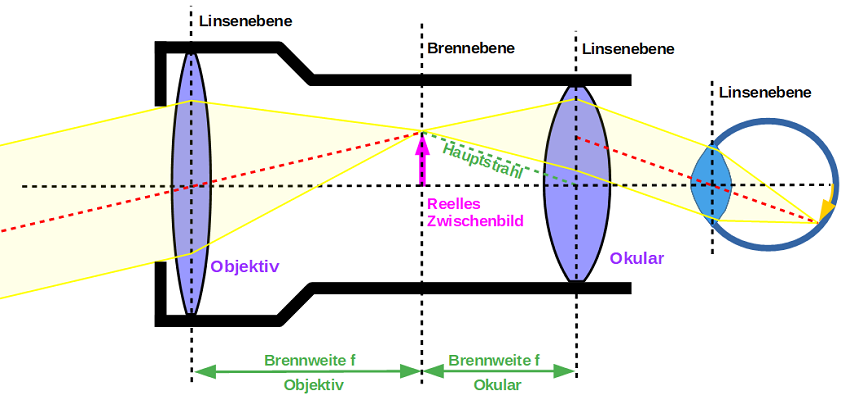
Zur Beobachtung entfernter Sterne benutzt man seit eh und je Fernrohre. Das sogenannte Kepler-Fernrohr oder auch astronomisches Fernrohr wurde um 1611 entwickelt und besteht aus zwei Sammellinsen unterschiedlicher Brennweiten. Dabei erzeugen die parallel einfallenden Lichtstrahlen ein reelles Zwischenbild des weit vom Fernrohr entfernten Gegenstandes in der Brennebene der Objektivlinse (größere Brennweite). Dieses Zwischenbild kann dann durch eine Okularlinse (kleinere Brennweite) vergrößert wie mit einer Lupe betrachtet werden. Dazu muss das Okular eben so eingestellt werden, dass das reelle Zwischenbild genau in der Brennebene der Okularlinse liegt.
In der Geschichte der Astronomie spielt die Entwicklung unterschiedlicher Fernrohre eine entscheidende Rolle. Das astronomische Fernrohr war im Mittelalter von hoher Bedeutung bei der Beobachtung der Sterne.
Mikroskop
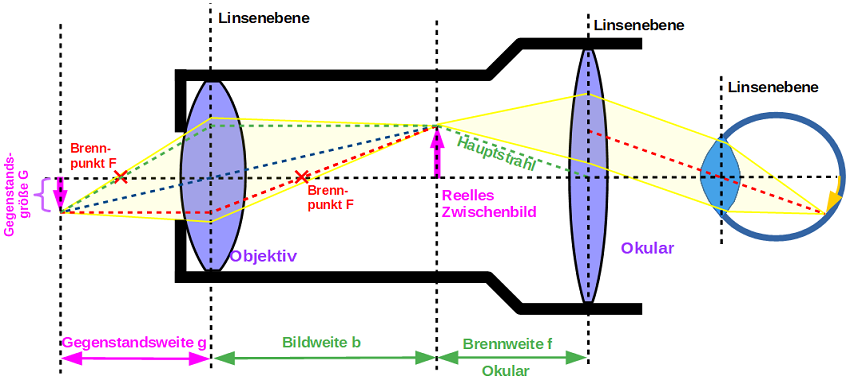
Das Mikroskop ist von der Bauweise her dem Kepler-Fernrohr sehr ähnlich. Wieder wird ein Gegenstand mit zwei Sammellinsen abgebildet, allerdings liegt der Gegenstand nicht in weiter Ferne, sondern ist diesmal klein und nur wenig von der Objektivlinse (kleinere Brennweite) entfernt. Diese erzeugt wiederum ein reeles Zwischenbild in der Bildweite b, das dann vom Okular (größere Brennweite) vergrößert wird.

Pierre de Fermat war nicht der Entdecker des Brechungsgesetzes aber es gelang ihm, einen mathematischen Beweis zu erbringen, dass man das Brechungsgesetz aus seinem Minimalprinzip der zeitlich kürzesten Lichtwege herleiten kann. Dieses so genannte Fermat´sche Prinzip lautet:
Von allen denkbaren möglichen Lichtwegen zwischen A und B, nimmt das Licht den Weg, der die kürzeste Zeit benötigt!
Aufgabe:
| Untersuche in allen unten aufgeführten Beispielen verschiedene Wege von A nach B. | |
| a) | Zeichne verschiedene Wege von A nach B über die Punkte P1 bis P7 mit dem Lineal ein. |
| b) | Mit Hilfe des Maßstabes und einem Lineal kann man Länge der verschiedenen Wege bestimmen. Bestimme die Weglängen in m und trage die Ergebnisse in die zugehörige Tabelle ein |
| c) | In Wasser kann man sich nur sehr langsam mit einer Geschwindigkeit von etwa 2 m/s bewegen. Am Strand hingegen kann man mit etwa 3 m/s laufen. Berechne die benötigte Zeit für alle eingezeichneten Wege zwischen A und B. Notiere die Ergebnisse in die Tabelle ein! |
| d) | Finde noch "bessere" Wege. Wähle dazu einen Punkt P8 auf der Grenzlinie zwischen Strand und Wasser, so dass noch ein zeitlich kürzerer Wege entstehen. Notiere die Weglänge und benötigte Zeit in der noch leeren Spalte. |
| e) | Markiere in den Tabellen durch Umkreisen die kürzesten Wege in "rot" und die zeitlich kürzesten Wege in "grün"! |
| f) | Vergleiche alle Ergebnisse mit den Erkenntnissen aus der Strahlenoptik. Was fällt auf? |
Beispiel 1:
Situation: Max will von A aus das Lagerfeuer bei B löschen. Er rennt also zum Wasser und füllt einen Eimer mit Löschwasser. Welcher Weg ist der zeitlich kürzeste von A über das Wasser zu B?
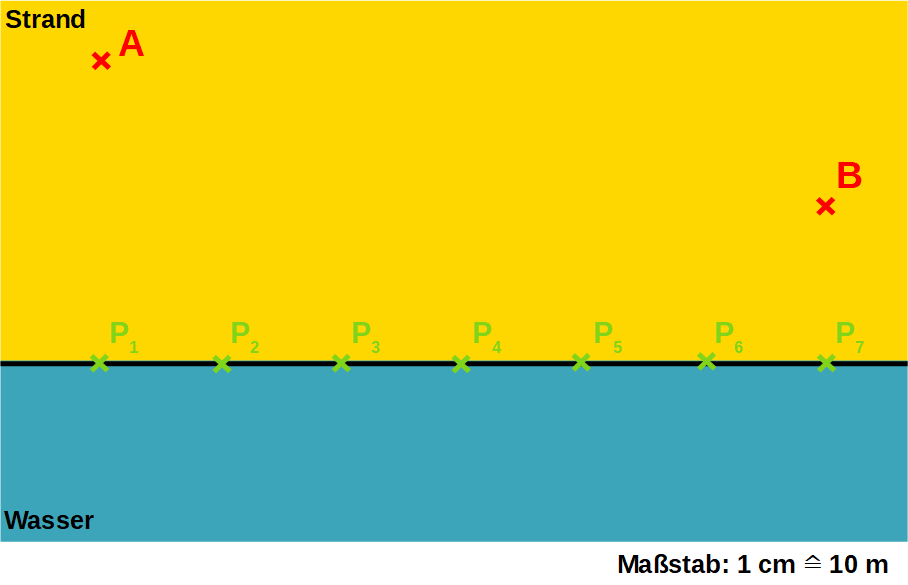
Tabelle Weglängen:
| Weg über P1 | Weg über P2 | Weg über P3 | Weg über P4 | Weg über P5 | Weg über P6 | Weg über P7 | Weg über P8 | |
| Weglänge 1 in m von A zum Wasser | ||||||||
| Weglänge 2 in m vom Wasser zu B | ||||||||
| Weglänge gesamt in von A nach B: |
Tabelle Benötigte Zeit:
| Weg über P1 | Weg über P2 | Weg über P3 | Weg über P4 | Weg über P5 | Weg über P6 | Weg über P7 | Weg über P8 | |
| Zeit 1 in s von A zum Wasser | ||||||||
| Zeit 2 in s vom Wasser zu B | ||||||||
| Zeit gesamt in von A nach B: |
Beispiel 2:
Situation: Max will als Rettungsschwimmer von A aus eine Person bei B aus dem Wasser retten. Welcher Weg ist der zeitlich kürzeste von A nach B?
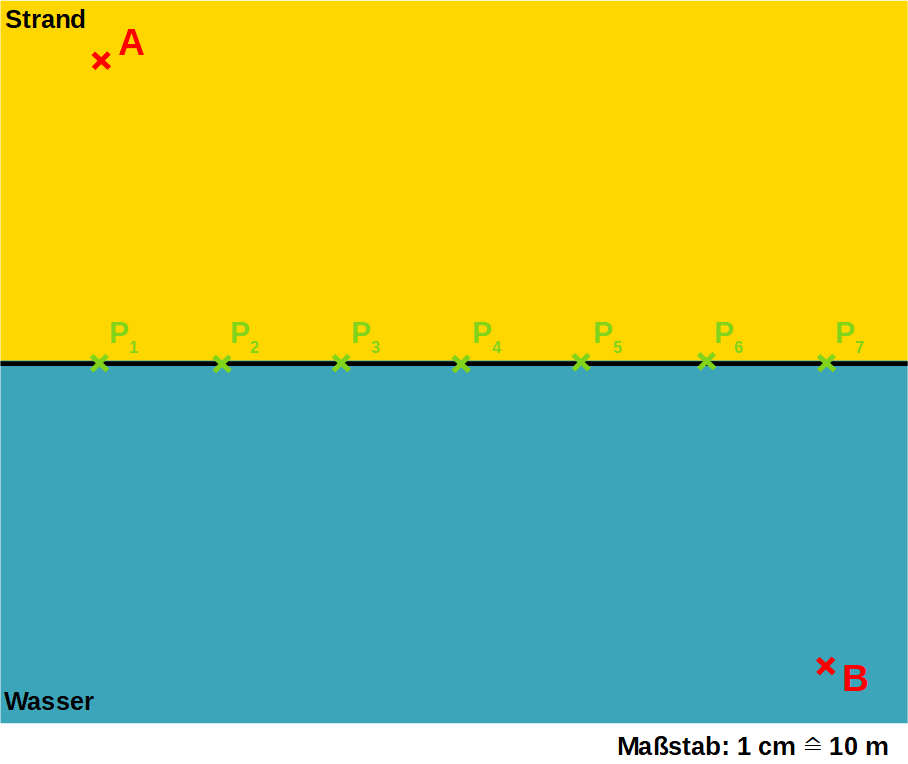
Tabelle Weglängen:
| Weg über P1 | Weg über P2 | Weg über P3 | Weg über P4 | Weg über P5 | Weg über P6 | Weg über P7 | Weg über P8 | |
| Weglänge 1 in m von A am Strand | ||||||||
| Weglänge 2 in m nach B im Wasser | ||||||||
| Weglänge gesamt in von A nach B: |
Tabelle Benötigte Zeit:
| Weg über P1 | Weg über P2 | Weg über P3 | Weg über P4 | Weg über P5 | Weg über P6 | Weg über P7 | Weg über P8 | |
| Zeit 1 in s von A am Strand | ||||||||
| Zeit 2 in s nach B im Wasser | ||||||||
| Zeit gesamt in von A nach B: |
Beispiel 3:
Situation: Max will von A aus zu seinem Zelt bei B auf der anderen Seite des Wassergrabens. Welcher Weg ist der zeitlich kürzeste von A durch den Wassergraben nach B?
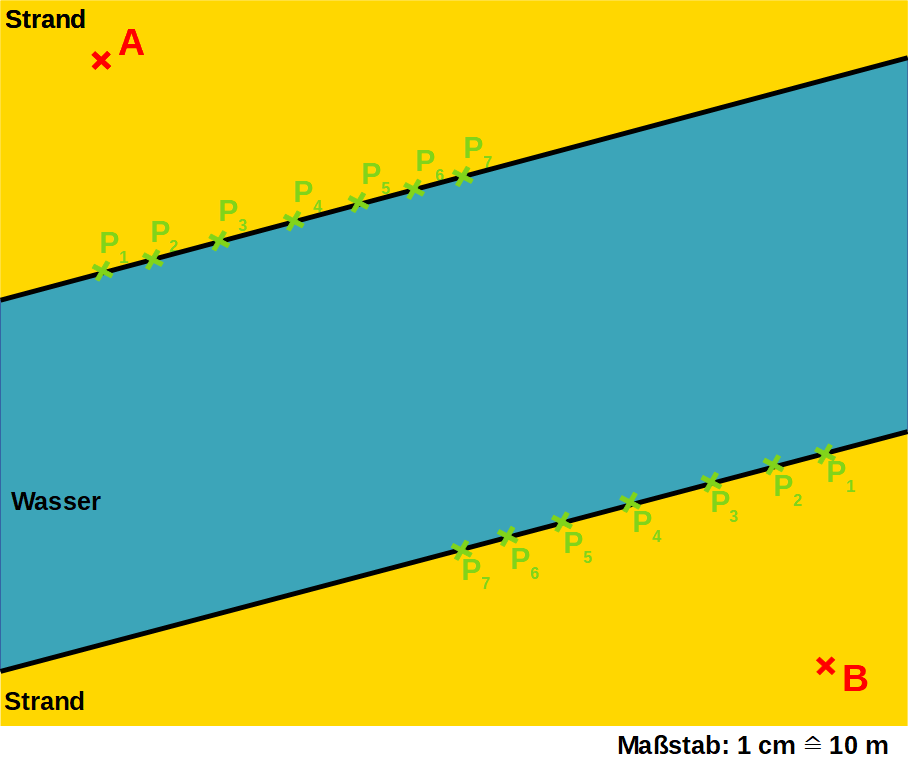
Tabelle Weglängen:
| Weg über P1 | Weg über P2 | Weg über P3 | Weg über P4 | Weg über P5 | Weg über P6 | Weg über P7 | Weg über P8 | |
| Weglänge 1 in m von A zum Wasser | ||||||||
| Weglänge 2 in m im Wasser | ||||||||
| Weglänge 3 in m vom Wasser zu B | ||||||||
| Weglänge gesamt in von A nach B: |
Tabelle Benötigte Zeit:
| Weg über P1 | Weg über P2 | Weg über P3 | Weg über P4 | Weg über P5 | Weg über P6 | Weg über P7 | Weg über P8 | |
| Zeit 1 in s von A zum Wasser | ||||||||
| Zeit 2 in s im Wasser | ||||||||
| Zeit 3 in s vom Wasser zu B | ||||||||
| Zeit gesamt in von A nach B: |

Aufgaben zu den Grundlagen der Strahlenoptik:
Aufgabe 1: SchattenräumeAufgaben zu Lochkamera:
Aufgabe 6: KerzeAufgaben zu Linsen:
Aufgabe 11: Strahlengang bei Sammellinsen IAufgaben zu optischen Geräten:
Aufgabe 16: Linsenkamera