
 |
Kongruenzen |
|

Häufig kommt es beim Rechnen nicht darauf an, das genaue Ergebnis der Rechnung im Detail zu kennen. Meistens hat man es dann mit Situationen zu tun, die sich nach einer gewissen Anzahl von Durchläufen wiederholen, wie etwa die Uhrzeit oder die Wochentage in den obigen Beispielen. Bei vielen Fragestellungen reicht es dann aus, den „Ort“ zu kennen, bei dem man nach einer beliebigen Anzahl von Durchläufen „landet“. Die genaue Anzahl der Durchläufe ist dann uninteressant und kann außer acht gelassen werden. Auch beim Programmieren kommt es immer wieder zu Situationen, die sich nach gewissen Regeln wiederholen. Die sogenannte „Modulo-Rechnung“ stellt die mathematische Grundlagen für diese Art von Fragestellungen bereit und wird im folgende eingeführt und aufgebaut.
Grundlagen:Jede natürliche Zahl n kann m verschiedenen Teilmengen zugeteilt werden, denn jede natürliche Zahl n lässt bei der Division durch m eine der Zahlen 0, 1, 2, …., m-1 als wohldefinierten Rest. Interessant ist nun, in welche Teilmenge die Zahl n gehört. Für m = 6 gibt es die Teilmengen 0, 1, 2, 3, 4 und 5. Die natürliche Zahl 8 gehört in die Teilmenge 2, da die Division von 8 durch 6 den Rest 2 lässt. Ebenso gehört die 26 in diese Teilmenge. Mit Hilfe eines „Kreises“ oder einer „Kommode mit Schubladen“ kann die Einteilung der natürlichen Zahlen in ihre zugehörigen Teilmengen veranschaulicht werden.
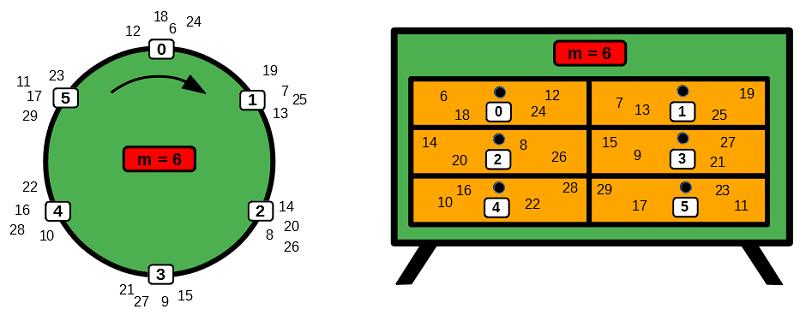
Untersucht man die Zahlen, die sich in einer Teilmenge (Schublade) befinden, so stellt man fest, dass die Differenz der Zahlen immer durch 6 teilbar ist. Außerdem erkennt man in der Kreisdarstellung, dass man sich beim Zählen im Uhrzeigersinn dreht. Diese Eigenschaften kann man verwenden, um auch negative ganze Zahlen eindeutig in ihre zugehörigen Teilmengen (Schubladen) einzuteilen. Hierzu zählt man von 0 beginnend gegen den Uhrzeigersinn weiter: Im Beispiel gehört die -1 also in die Teilmenge (Schublade) mit der Aufschrift 5, die -2 in die Schublade mit der Aufschrift 4, usw.
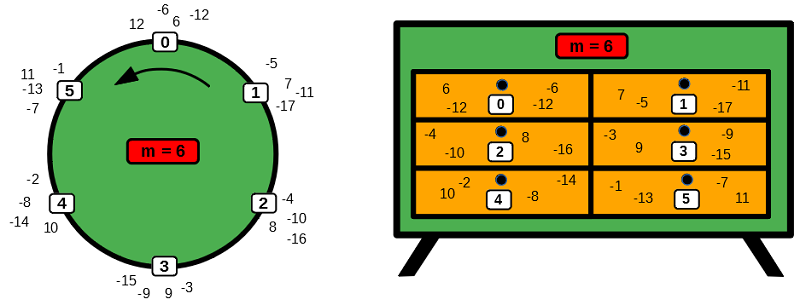
Die beschriebene Einteilung hat nun also für alle ganzen Zahlen folgende Besonderheiten:
| • | Alle ganzen Zahlen lassen sich in genau eine Teilmenge (Schublade) einteilen. |
| • | Beim Hochzählen dreht man sich in der Kreisdarstellung im Uhrzeigersinn, beim Runterzählen dreht man sich entgegen des Uhrzeigersinns. |
| • | Die Differenz zweier Zahlen aus der gleichen Teilmenge (Schublade) ist immer durch m teilbar. |
Diese Eigenschaften kann für folgende grundlegende Definition verwenden:
Definition:Zwei ganze Zahlen a und b heißen kongruent bezüglich m, wenn die Differenz a-b durch m teilbar ist. Die beiden Zahlen befinden sich dann in der gleichen Teilmenge bezüglich m.
Schreibweise:
a ≡ b mod m "a ist kongruent zu b modulo m"
Bemerkung:
Die vier Aussagen sind gleichwertig:
| • | a ≡ b mod m |
| • | m teilt die Differenz a - b |
| • | Es existiert ein k ∈ ℕ, sodass gilt: k ⋅ m = a - b (k beschreibt die Anzahl der Drehungen). |
| • | a und b sind in der gleichen Teilmenge. |
| Erste anschauliche Anwendungen der Rechnung mit Kongruenzen „modulo m“ kann man bei Problemen zu Uhrzeiten, Wochentagen oder Jahrestagen entdecken. Ein Tag hat 24 Stunden, deshalb liegt die Kongruenz „modulo 24“ nahe. Startet man etwa einen 22-stündigen Flug um 7:00 Uhr, so landet man ohne Zeitverschiebung um 5:00 Uhr morgens (Erklärung: 7 + 22 = 29 und 29 ≡ 5 mod 24). Alle 7 Tage wiederholt sich auch der Wochentag, aus diesem Grund ist die Kongruenz bezüglich des zum Moduls 7 einleuchtend. Beginnt die 40-tägige Fastenzeit etwa an einem Montag, so endet sie an einem Samstag (Erklärung: 40 ≡ 5 mod 7, also 5 Tage nach einem Montag). Bei Rechnungen zu Jahrestagen kommen Kongruenzen „modulo 365“ ins Spiel, denn ein Jahr (kein Schaltjahr) hat eben 365 Tage. Fällt etwa Weihnachten auf einem Sonntag, so ist im Jahr darauf (kein Schaltjahr) Weihnachten an einem Montag (Erklärung: 365 ≡ 1 mod 7) |  |
Durch die Kongruenz „modulo m“ werden zwei ganze Zahlen in Verbindung gebracht. Haben sie bei der Division durch m den gleichen Rest, so sagen wir, diese beiden Zahlen sind kongruent. Auch Dreiecke können in Verbindung gebracht werden. Stimmen zwei Dreiecke etwa in allen Seitenlängen überein, so sagt man ebenso, dass diese beiden Dreiecke kongruent sind (Achtung: Die Dreiecke sind nicht „gleich“, denn sie können sich ja in den Bezeichnungen der Ecken unterscheiden). Eine Verbindung kann auch bei zwei Geraden hergestellt werden. Sind zwei Geraden parallel, so stehen sie in einer besonderen Verbindung zueinander. Betrachtet man die Menge der Menschen, so wäre eine mögliche Verbindung die „Verwandtschaft“. Sandra und Mark sind Geschwister und miteinander verwandt.
Diese verschiedenen Beispiele zeigen, dass zwei Elemente einer Menge in einer bestimmten Beziehung zueinander stehen können. Mathematiker interessieren sich nun für die prinzipiellen Eigenschaft dieser Beziehungen. Man spricht von einer Äquivalenzrelation, falls die Beziehung die folgenden drei Eigenschaften besitzt:
| • | Reflexivität: | Das Element a steht zu sich selber in dieser besonderen Verbindung. |
| • | Symmetrie: | Wenn das Element a zu b in dieser besonderen Beziehung steht, dann steht auch b zu a in dieser besonderen Verbindung. |
| • | Transitivität: | Wenn das Element a zu b in dieser besonderen Beziehung steht und b auch zu c, dann steht auch a zu c in dieser besonderen Verbindung. |
Die Kongruenz „modulo m“ ist eine Äquivalenzrelation, denn die drei oben beschriebenen Eigenschaften werden erfüllt:
| • | Reflexivität: | a ≡ a mod m, denn die Differenz a – a ist durch m teilbar. a und a lassen also bei der Division durch m den gleichen Rest. |
| • | Symmetrie: | Wenn a ≡ b mod m, dann heißt das, das die Differenz a – b durch m teilbar ist. Dann ist aber auch die Differenz b – a durch m teilbar. Also gilt: b ≡ a mod m. |
| • | Transitivität: | Wenn a ≡ b mod m und b ≡ c mod m, dann teilt m die Differenzen ( a – b ) und ( b – c ). Dann teilt aber m auch die Summe ( a – b ) + ( b – c ) = a – c. Also gilt: a ≡ c mod m. |
Mit Kongruenzen kann man fast so rechnen wie mit den ganzen Zahlen. Schon mit wenigen Rechenregeln können viele Aufgaben stark vereinfacht oder gar gelöst werden.
Es sei a ≡ b mod m und c ≡ d mod m. Dann gelten die folgenden Rechenregeln:
| • | Addition: | a + c ≡ b + d mod m |
| • | Subtraktion: | a - c ≡ b - d mod m |
| • | Multiplikation: | a ⋅ c ≡ b ⋅ d mod m |
Beispiele:
| 1) | Es gilt: 116 ≡ 1 mod 23 und 22 ≡ 1 mod 23. Also gilt nach den obigen Rechenregeln: | |
| 138 = 116 + 22 ≡ 1 + ( - 1 ) = 0 mod 23 | ||
| 94 = 116 - 22 ≡ 1 - ( - 1 ) = 2 mod 23 | ||
| 2552 = 116 ⋅ 22 ≡ 1 ⋅ ( - 1 ) = - 1 mod 23 | ||
| 2) | Es gilt: 11 ≡ 1 mod 10. Also gilt nach den obigen Rechenregeln: | |
| 112 = 11 ⋅ 11 ≡ 1 ⋅ 1 = 1 mod 10 | ||
| 11k = 11 ⋅ 11 ⋅....⋅ 11 ≡ 1 ⋅ 1 ⋅....⋅ 1 = 1 mod 10 | ||
| „Alle Potenzen der Zahl 11 enden auf 1“ | ||
Beweise:
Exemplarisch seien hier die Beweise für die Addition und die Multiplikation aufgeführt. Der Beweis für die Rechenregeln der Differenz kann analog zum Beweis für die Addition geführt werden.
| • | Addition: | Wenn a ≡ b mod m und c ≡ d mod m, so teilt m die Differenzen (a - b) und (c - d) |
| Wenn m die Differenzen (a - b) und (c - d) teilt, so teilt m auch die Summe (a – b) + (c – d) | ||
| Umsortieren ergibt: a – b + c – d = a + c – b – d = (a + c) – (b + d) | ||
| Also teilt m auch (a + c) – (b + d) und somit ist a + c ≡ b + d mod m | ||
| • | Multiplikation: | Wenn a ≡ b mod m und c ≡ d mod m, so teilt m die Differenzen (a - b) und (c - d) |
| Wenn m die Differenzen (a - b) und (c - d) teilt, so teilt m auch die Produkte (a – b)⋅c und b⋅(c – d) | ||
| Also teilt m auch die Summe (a – b)⋅c + b⋅(c – d) | ||
| Ausmultiplizieren und umsortieren ergibt: (a – b)⋅c + b⋅(c – d) = a⋅c – b⋅c + b⋅c – b⋅d = a⋅c – b⋅d | ||
| Also teilt m auch (a⋅c) – (b⋅d) und somit ist a ⋅ c ≡ b ⋅ d mod m |
„Jonas hat eine Tüte Gummibärchen gekauft, aber er weiß nicht, wie viele Gummibärchen in er Tüte sind. Wenn er sie aber in 5er-Häufchen aufteilt, so bleiben 3 Gummibärchen übrig. Teilt er sie in 7er-Häufchen auf, so bleiben 2 übrig. Wie viele Gummibärchen waren es wohl in der Tüte?“
Von der unbekannten Anzahl x an Gummibärchen weiß man also nur, dass die Anzahl x bei der Division durch 5 den Rest 3 lässt und bei der Division durch 7 den Rest 2. Die Anzahl x soll also zeitgleich die zwei Kongruenzen
x ≡ 3 mod 5 und x ≡ 2 mod 7
erfüllen. Ein Lösung für solche Fragenstellungen liefert der sogenannte „Chinesische Restsatz“. Er geht auf verschiedene chinesischen Mathematiker zurück. In einer vereinfachten Form lautet er:
Chinesischer Restsatz:
Gesucht ist eine Zahl x, die sowohl die Kongruenz x ≡ p mod m als auch die Kongruenz x ≡ q mod n gleichzeitig erfüllt, wobei m und n teilerfremd seien!
| 1) | Die Zahl x = a⋅p⋅n + b⋅q⋅m mit a⋅n ≡ 1 mod m und b⋅m ≡ 1 mod n ist kongruent zu p mod m und q mod n, erfüllt als beide Kongruenzen simultan. |
| 2) | Die kleinste Zahl x, die beide Kongruenzen simultan erfüllt, kann über x ≡ a⋅p⋅n + b⋅q⋅m mod (m⋅n) berechnet werden. |
Beispiel:
| Gesucht: | x mit x ≡ 3 mod 5 und x ≡ 2 mod 7 (5 und 7 sind teilerfremd!) |
| Also: p = 3 m = 5 q = 2 n = 7 | |
| Gesucht: | a mit a⋅n ≡ 1 mod m Hier: a⋅7 ≡ 1 mod 5 ⇒ a = 3 |
| Gesucht: | b mit b⋅m ≡ 1 mod n Hier: b⋅5 ≡ 1 mod 7 ⇒ b = 3 |
| x = a⋅p⋅n + b⋅q⋅m = 3⋅3⋅7 + 3⋅2⋅5 = 63 + 30 = 93 | |
| Kleinste Zahl: x ≡ a⋅p⋅n + b⋅q⋅m mod (m⋅n) Hier: 23 ≡ 93 mod 35 | |
| Probe: | 23 ≡ 3 mod 5 ✓ und 23 ≡ 2 mod 7 ✓ |
| Antwort: | 23 ist die kleinste natürliche Zahl, die beide Kongruenzen simultan erfüllt. Es könnten also 23 Gummibärchen in der Tüte gewesen sein. |
Die Rechnung mit Kongruenzen „modulo m“ wird beim Programmieren relativ häufig verwendet. Sehr einfach kann beispielsweise mit Hilfe des Modulo-Operators überprüft werden, ob eine Zahl gerade ist. Außerdem kann die Modulo-Anweisung verwendet werden, wenn Schleifen lediglich bei jedem n-ten Durchlauf eine spezielle Abfolge von Anweisungen ausführen soll. Häufig wird der Modulo-Operator auch zur Codierung von Abbruchbedingungen von Schleifen verwendet. Allgemein kann man mit der Modulo-Rechnung überprüfen, ob eine Zahl durch eine andere teilbar ist. Weitere Anwendungen zeigen die folgenden Beispiele:
Binärdarstellung:
| Für einen Algorithmus zur Umwandlung einer natürlichen Zahl n in ihre Binärdarstellung kann man die Kongruenz „modulo 2“ verwenden. Das Struktogramm zeigt hierzu ein Beispiel: |  |
Euklidischer Algorithmus:
| Auch der Euklidische Algorithmus zur Bestimmung des größten gemeinsamen Teilers zweier Zahlen a und b kann mit Hilfe des Modulo-Operators programmiert werden. Das Struktogramm zeigt wiederum ein Beispiel: | 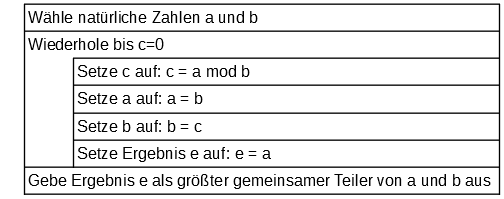 |
Prüfziffern:
| Auf zahlreichen Waren befindet sich auf der Verpackung eine Nummer, die das Produkt eindeutig identifiziert. Insbesondere im Buchhandel ist jedes Druckerzeugnis mit einer sogenannten ISBN-13-Nummer versehen. An dieser Nummer kann man verschiedene Informationen zum Buch – wie etwa Verlag oder Sprache – erkennen. Die letzte Ziffer der ISBN-13-Nummer ist eine sogenannte Prüfziffer. Sie errechnet sich nach einem festgelegten Verfahren aus den vorherigen 12 Ziffern. Wenn sich nun nach einer Übermittlung der ISBN-13-Nummer – etwa beim Eintippen oder Scannen – diese Zahl nicht aus den übrigen ergibt, so muss es zu einem Übertragungsfehler gekommen sein. Zur Kontrolle, ob eine übertragene ISBN-13-Nummer korrekt ist, werden alle 13 Ziffern aufaddiert, wobei die Ziffern mit gerader Position (also die Ziffern 2, 4, 6, …. ) jeweils vor der Addition mit 3 multipliziert werden. Ist diese Summe dann durch 10 teilbar, so ist die ISBN-13-Nummer korrekt. Das Struktogramm stellt eine Algorithmus zur Überprüfung einer ISBN-13-Nummer dar.: | 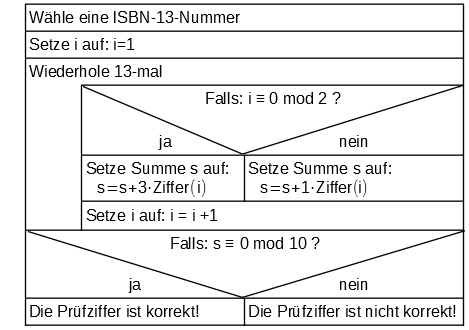 |

Ein Zuschauer wählt aus einem gemischten Stapel von 45 verschiedenen Spielkarten eine beliebige Karte aus, die er sich merkt (hier: z.B. die ❤ 10 ). Anschließend findet der Zauberer genau diese Karte.

Nachdem der Zuschauer die Karte gewählt hat, kann der Stapel erneut verdeckt gemischt werden. Anschließend darf die Reihenfolge der Karten allerdings nicht mehr durcheinander gebracht werden! Die oberste Karte im verdeckten Stapel ist nun die Karte mit der Nummer 1, dann kommt die Karte Nummer 2, usw.

Nun werden die Karten nach und nach offen in 9er-Reihen ausgelegt. Wenn alle Karten auf dem Tisch liegen, wird der Zuschauer gefragt, in welcher Spalte sich die gemerkte Karte befindet (Hier: Spalte 5). Der Zauberer merkt sich dabei die Nummer des Stapels, der vom Zuschauer genannt wurde.

Nachdem die entscheidende Spalte benannt wurde, werden die Karten wieder rückwärts aufgenommen und verdeckt auf den Stapel gelegt, sodass die Karten wieder in der gleichen Reihenfolge wie vorher liegen.
Nun werden die Karten erneut auf dem Tisch ausgelegt, aber dieses Mal in 5er-Stapeln. Der Zuschauer benennt abermals die Spalte, in der sich die gemerkte Karte befindet (Hier: Spalte 3).

Nun kann der Zauberer die Nummer der Karte berechnen, denn die gesuchte Kartennummer muss die folgenden Kongruenzen erfüllen (Die Spaltennummern entsprechen den Resten bei der Division durch 9 bzw. 5):
x ≡ 5 mod 9 und x ≡ 3 mod 5
Mit Hilfe des chinesischen Restsatzes können diese simultanen Kongruenzen gelöst werden.
Lösung:
| Gesucht: | x mit x ≡ 5 mod 9 und x ≡ 3 mod 5 (9 und 5 sind teilerfremd!) |
| Also: p = 5 m = 9 q = 3 n = 5 | |
| Gesucht: | a mit a⋅n ≡ 1 mod m Hier: a⋅5 ≡ 1 mod 9 ⇒ a = 2 |
| Gesucht: | b mit b⋅m ≡ 1 mod n Hier: b⋅9 ≡ 1 mod 5 ⇒ b = 4 |
| x = a⋅p⋅n + b⋅q⋅m = 2⋅p⋅5 + 4⋅q⋅9 = 10⋅p + 36⋅q = 10⋅5 + 36⋅3 = 50 + 108 = 158 | |
| Kleinste Zahl: x ≡ a⋅p⋅n + b⋅q⋅m mod (m⋅n) Hier: 23 ≡ 158 mod 45 | |
| Probe: | 23 ≡ 5 mod 9 ✓ und 23 ≡ 3 mod 5 ✓ |
| Antwort: | 23 ist die kleinste natürliche Zahl, die beide Kongruenzen simultan erfüllt. |

Die gesuchte Karte ist also die 23. Karte im verdeckten Stapel, also die gesuchte ❤ 10 . Sie wird nun vom Zauberer aufgedeckt.

Aufgaben zu Kongruenzen "modulo m":
Aufgabe 1: Kongruenzen I