
 |
Primzahlen |
|
Zwei, drei, fünf, sieben und elf – das sind die ersten Natürlichen Zahlen, die größer als 1 sind und nicht durch andere Natürlichen Zahlen geteilt werden können, sogenannte Primzahlen. Auf den ersten Blick eine einfache Sache. Dennoch stecken für Zahlentheoretiker bis heute noch viele Rätsel in der Menge der Primzahlen. Warum treten sie beispielsweise manchmal häufiger auf und dann wieder ohne erkennbaren Grund seltener? Oder wie kann man möglichst schnell die Primfaktoren großer Natürlicher Zahlen bestimmen? Insbesondere im Bereich der Verschlüsselungstechnik, der sogenannten Kryptographie spielen bis heute Primzahlen eine entscheidende Rolle.
Eine grundlegende Aussage der Mathematik ist der Fundamentalsatz der Arithmetik: Jede Natürliche Zahl größer 1, die selber keine Primzahl ist, kann bis auf die Reihenfolge der Faktoren eindeutig und unverwechselbar als Produkt von Primzahlen – sogenannten Primfaktoren – zusammengesetzt oder geschrieben werden. Genau aus diesem Grund werden Primzahlen auch oft als die „Bausteine“ oder „Atome“ der Mathematik bezeichnet oder mit den „Elementen“ in der Chemie verglichen.
Dass es unendliche viele Primzahlen gibt, wusste man schon in der Antike. Euklid konnte einen logischen Beweis anführen, der zeigen konnte, dass jede theoretische Liste von Primzahlen – sei sie auch noch so groß – nicht alle Primzahlen enthalten kann. Mit einem einfachen Trick lässt sich nämlich aus jeder denkbaren Primzahlenliste eine neue Primzahl errechnen, die nicht in der Liste ist. Damit ist sicher gestellt: Die Anzahl der Primzahlen ist unendlich!
Auch wenn heute Computer die Arbeit von Mathematikern enorm unterstützen können, so ist bis heute noch keine Methode gefunden worden, die in einer realitätsnahen Zeit die Primfaktoren von wirklich großen Zahlen bestimmen könnte. Auch Großrechner benötigen hierzu bei Zahlen mit etwa hundert Stellen schon mehrere Jahrhunderte. Umgekehrt aber können Computer schnell mehrere Primfaktoren miteinander multiplizieren. Genau diesen Unterschied im Berechnungsaufwand nutzt man heutzutage beim Verschlüsseln von Nachrichten und Geheimzahlen aus, dem sogenannten RSA-Verfahren, eine sehr spannende Anwendung der doch auf den ersten Blick sehr „einfachen“ Primzahlen!
Definitionen und Festlegungen:In einem ersten Schritt müssen aber einige Begriffe genau definiert werden. Die wichtigste Definition in diesem Abschnitt ist die der Primzahl. Sie lautet:
Eine Natürliche Zahl, die genau zwei Teiler hat - 1 und sich selber - wird "Primzahl" genannt!
Nach dieser Festlegung ist 1 also keine Primzahl, denn 1 hat nur einen Teiler! Und das ist auch gut so! Denn sonst wäre die oben beschriebene Zerlegung einer Natürlichen Zahl in ihre Primfaktoren nicht mehr eindeutig (3 ⋅ 5 ⋅ 11 = 3 ⋅ 1 ⋅ 5 ⋅ 1 ⋅ 11). Es gibt auch noch weitere mathematische Gründe, warum man sich innerhalb der Mathematik seit Beginn des 20. Jahrhunderts darauf geeinigt hat, die 1 nicht als Primzahl anzusehen.
Wenn aber nun eine Natürliche Zahl keine Primzahl ist, so kann sie durch eine andere Natürliche Zahlen geteilt werden. Die genaue Festlegung, was ein Teiler ist, lautet folgendermaßen:
Eine Natürliche Zahl t heißt "Teiler" der Natürlichen Zahl n, wenn eine weitere Natürliche Zahl k existiert, sodass man n als Produkt der Zahlen k und t schreiben kann.
Wenn also t ein Teiler von n ist, dann ergibt die Division von n durch t keinen Rest.
Wie erkennt man nun, ob eine Natürliche Zahl eine Primzahl ist oder sich eben in Primfaktoren zerlegen lässt?Bei kleineren Natürlichen Zahlen ist das in der Praxis keine Problem! Durch Kopfrechnen erkennt man schnell, dass sich 21 in die Primfaktoren 3 und 7 zerlegen lässt! Außerdem weiß man auch, dass 17 oder 19 Primzahlen sind. Wie kann man aber systematischer Vorgehen?
Das Sieb des Eratosthenes:
Will man eine Liste der ersten Primzahlen erstellen, so gibt es ein Verfahren, das auf den griechischen Gelehrten Eratosthenes zurückgeht. Da bei dieser Methode alle Nicht-Primzahlen ausgestrichen werden und nur noch Primzahlen übrig bleiben, nennt man dieses Verfahren auch „Sieb des Eratosthenes“. In einem ersten Schritte werden dazu alle Natürlichen Zahlen von 1 bis sagen wir 100 aufgeschrieben. Dann wird die Zahl 1 gestrichen, sie ist ja keine Primzahl. Die nächst größere Zahl - die 2 - wird umkreist und dann alle Vielfachen von ihr gestrichen. Dann wird die nach der 2 nächste nicht gestrichene Zahl - hier die 3 - umkreist und alle Vielfachen von ihr gestrichen. Jetzt wird die nach der 3 nächste freie Zahl umkreist - die 5 - und ihre Vielfachen gestrichen, usw. Nach wenigen Schritten sind alle Primzahlen umkreist und die zusammengesetzten Zahlen gestrichen!
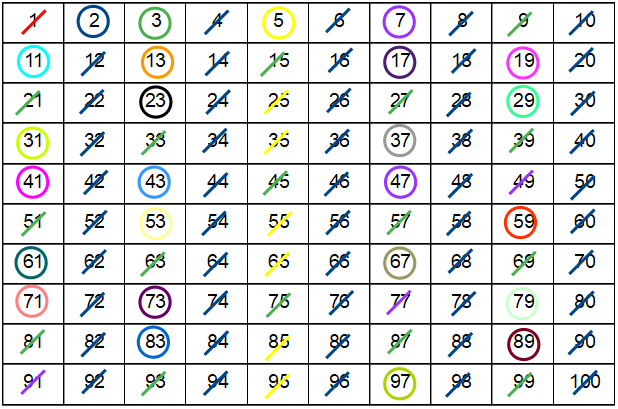
Ergebnis:
Die Primzahlen bis 100 lauten: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 und 97.
Dieses Verfahren kann auch leicht als Algorithmus mit einem Computer programmiert werden und liefert geschickt eine vollständige Liste der Primzahlen. Aber man kann sich leicht vorstellen, dass dieses Verfahren bei größeren Natürlichen Zahlen an seine Grenzen stößt. Wie kann beispielsweise eine einzelne sehr große Natürliche Zahl als Primzahl oder zusammengesetzte Zahl erkannt werden?
Die Teilbarkeitsregeln:
Hierbei helfen die sogenannten Teilbarkeitsregeln: Ist beispielsweise die Quersumme einer Natürlichen Zahl n durch 3 teilbar, dann ist auch diese Zahl n selber durch 3 teilbar und kann also keine Primzahl sein. Ein Vielzahl von weiteren Teilbarkeitsregeln, die leicht recherchiert werden können, stellen ein einfaches Hilfsmittel zum Finden von Teilern dar. Dabei kann man zwei Gruppen von Regeln unterscheiden: Bei Quersummenregeln benutzt man die Quersumme zur Überprüfung wie im oberen Beispiel, bei Endstellenregeln hingegen untersucht man eine bestimmte Anzahl von letzten Stellen der Natürlichen Zahl, um eine Aussage über die Teilbarkeit zu machen. Ist zum Beispiel die Zahl aus den letzten zwei Ziffern einer beliebigen Natürlichen Zahl n durch 4 teilbar, so ist auch die Zahl n selber durch 4 teilbar.
In manchen Fällen helfen auch die Summen- oder Produktregel bei der Untersuchung der Teiler von größeren Natürlichen Zahlen. Sie lauten:
Summenregel: Wenn sowohl a als auch b den Teiler t haben, dann hat auch a + b den Teiler t.
Produktregel: Wenn a oder b den Teiler t hat, dann hat auch a ⋅ b den Teiler t.
Alle diese Regeln müssen natürlich mathematisch fehlerfrei bewiesen werden. Nur so können sie in ihrer Allgemeingültigkeit verwendet werden.
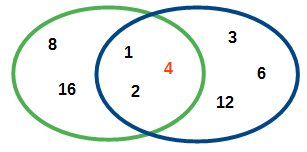
Hat man alle Teiler einer Natürlichen Zahl gefunden, so fasst man diese gerne in der Teilermenge zusammen. Das ist also eine Menge, in der alle Zahlen enthalten sind, durch die man diese Zahl teilen kann, ohne dass ein Rest bleibt. Zwei Beispiele:
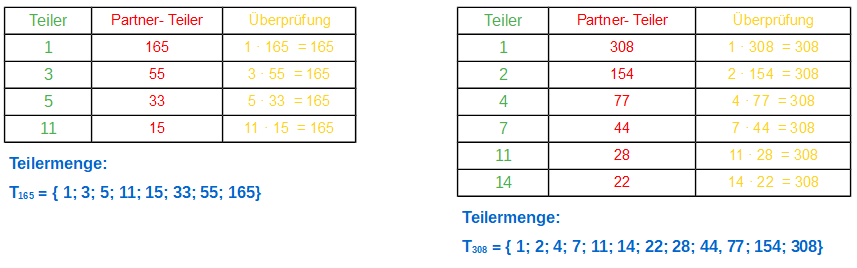
Dazu eine Bemerkung: Quadratzahlen haben eine ungerade Anzahl von Teilern, da ein Teiler zweimal – als Teiler und auch als Partner-Teiler – vorkommt und Nicht-Quadratzahlen haben eine gerade Anzahl von Teilern, da wie oben ersichtlich jeder Teiler auch einen Partner-Teiler hat.
Dennoch bleibt es schwer, die Primfaktoren schnell und zuverlässig zu berechnen. Auch Computern gelingt das bei riesigen Natürlichen Zahlen mit überschaubarem Rechenaufwand bis heute nicht!
Primfaktorzerlegung:Durch sinnvolles Testen in Einzelschritten kann man die Primfaktoren einer geläufigen beliebigen Natürlichen Zahl bestimmen. Das Verfahren beginnt mit der kleinsten Primzahl, der 2. Ist die Natürliche Zahl durch 2 teilbar, so hat man den ersten Primfaktoren bereits gefunden. Im folgenden wird nun der „Rest“ untersucht. Ist dieser abermals durch 2 teilbar, so hat man den zweiten Primfaktor, wiederum die 2. Ansonsten überprüft man, ob der „Rest“ durch die nächst größere Primzahl – hier die 3 – teilbar ist. Nach und nach werden so alle Primzahl getestet. Dabei wird bei jedem Schritt der „Rest“ immer kleiner, bis der „Rest“ eine Primzahl ist. Somit hat man alle Primfaktoren gefunden. Sortiert man diese der Größe nach, so erhält man ein eindeutiges Ergebnis, hier ein Beispiel:

Sowohl die Teilermenge als auch die Primfaktorzerlegung einer Natürlichen Zahl lassen sich übersichtlich in einem sogenannten Hasse-Diagramm oder Teilerbild darstellen!
Die zwei Beispiele verdeutlichen dies:
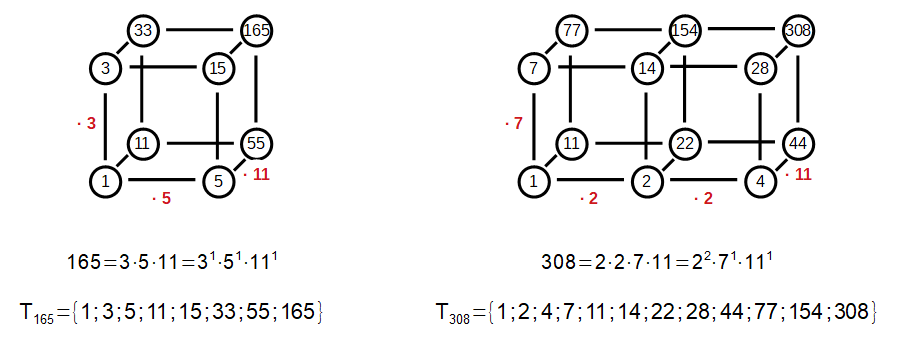
Dabei entspricht jeder Primzahl eine "Dimension" im Hasse-Diagramm. Kommt ein Primfaktor mehrfach in der Primfaktorzerlegung vor, so hat das Hasse-Diagramm in der zugehörigen "Dimension" mehrere Stufen. Die Knoten werden von den Teilern gebildet.
Größter gemeinsamer Teiler und kleinstes gemeinsames Vielfaches:Innerhalb der Zahlentheorie spielen zwei mathematische Grundbegriffe eine wichtige Rolle: der „größte gemeinsame Teiler“ (ggT) und das „kleinste gemeinsame Vielfache“ (kgV). Dabei ist der ggT zweier ganzer Zahlen die größte Zahl, durch die beide Zahlen teilbar sind. Das kgV zweier ganzer Zahlen hingegen ist die kleinste Zahl, die sowohl Vielfaches von der einen als auch Vielfaches von der anderen Zahl ist. Zwei Beispiele:
| größter gemeinsamer Teiler (ggT) | kleinstes gemeinsames Vielfaches (kgV) |
| Die Teiler von 16 sind: 1, 2, 4, 8, 16 Die Teiler von 12 sind: 1, 2, 3, 4, 6, 12 Die gemeinsamen Teiler sind: 1, 2, 4 Der größte gemeinsamen Teiler von 16 und 12 ist also 4 | Die Vielfachen von 16 sind: 16, 32, 48, 64, 80, 96, 112,... Die Vielfachen von 12 sind: 12, 24, 36, 48, 60, 72, 84, 96, 108,... Die gemeinsamen Vielfachen sind: 48, 96,... Das kleinste gemeinsame Vielfache von 16 und 12 ist also 48 |
 | 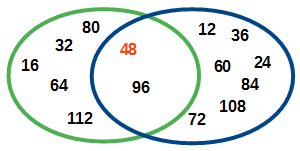 |
| Kurz: ggT(16;12)=4 | Kurz: kgV(16;12)=48 |
Gibt es bei zwei Zahlen a und b keinen gemeinsamen Teiler außer der 1 ( ggt(a;b) = 1 ), so sagt man, die beiden Zahlen a und b sind "teilerfremd". Zwei verschiedene Primzahlen sind natürlich stets teilerfremd. Aber auch die beiden Nicht-Primzahlen 21 und 55 sind teilerfremde Zahlen, kurz: ggt(21;55) = 1 .
Zwischen dem ggT und dem kgV zweier Zahlen a und b gibt es einen wichtigen, erstaunlichen Zusammenhang: das Produkt der Zahlen a und b ist stets gleich dem Produkt vom ggT und vom kgV dieser beiden Zahlen. Im obigen Beispiel in der Tablle war der ggT der beiden Zahlen 4, das kgV hingegen 48. Tatsächlich ist das Produkt von 12 und 16 genau 192 und damit gleich dem Produkt von 4 und 48 ( 12 ⋅ 16 = 192 = 4 ⋅ 48 = ggt(12;16) ⋅ kgV(12;16) ).
a ⋅ b = ggt(a;b) ⋅ kgV(a;b)
Zahlreiche mathematische Aufgaben und Probleme können mit Hilfe der beiden Begriffe gelöst werden. Zwei Beispiel:
1. Bei einer Maschine muss beispielsweise alle 24 Monate das Öl gewechselt werden, alle 84 Monate die Zahnräder ausgetauscht werden und alle 56 Monate der Keilriemen erneuert werden. Will man nun wissen, nach welcher Zeit alle drei Arbeiten gleichzeitig gemacht werden können, so sucht man in diesem Beispiel das kleinste gemeinsame Vielfache dieser drei Zahlen.
2. Die Aula einer Schule ist 30 m lang und 27 m breit. Der Boden soll mit möglichst großen quadratischen Fliesen belegt werden. Wie groß dürfen diese Fliesen dabei sein, wenn man keine Fliese zerschneiden möchte? Hier kann die Aufgabe mit Hilfe des größten gemeinsamen Teilers gelöst werden.

Ein Zuschauer wird aufgefordert, eine zweistellige Primzahl auszuwählen, die - etwa an einer Tafel - notiert wird. In Windeseile kann der Zauberer natürlich die beiden Teiler dieser Primzahl nennen. So weit, so gut! Nun wird aber die ausgewählte Primzahl viermal hintereinander notiert, sodass eine achstellige Zahl entsteht. Nun behauptet der Zauberer, dass er ebenso ohne viel nachzudenken blitzschnell einige Teiler dieser achtstelligen Zahl im Kopf berechnen kann.

Nachdem die achtstellige Zahl an der Tafel notiert ist, nennt der Zauberer rasant einige Teiler dieser großen Zahl und notiert sie an der Tafel. Diese können von den Zuschauern mit Hilfe eines Taschenrechners als Teiler überprüft werden. Die untere Auflistung ist nicht vollständig; es gibt noch weitere Teiler!

Erklärung:
Hat man eine zweistellige Primzahl p ausgewählt, so entspricht das viermalige Hintereinander-Schreiben zu einer achtstelligen Zahl einer Multiplikation mit der Zahl 1010101. Hier:
67 ⋅ 1010101 = 67676767
Interessant ist dabei der Faktor 1010101, denn er kann in genau drei Primzahlen 73, 101 und 137 zerlegt werden. Es gilt also:
1010101 = 73 ⋅ 101 ⋅ 137
Dadurch kennt man auch die Primfaktorzerlegung einer jeden wie oben gebildeten achtstelligen Zahl, denn ist der Faktor 1010101 durch 73 teilbar, so ist auch die achtstellige Zahl durch 73 teilbar. Da die zweistellige Zahl als Primzahl vorausgesetzt war lautet die Primfaktorzerlegung der achtstelligen Zahl in diesem Beispiel:
67676767 = 67 ⋅ 73 ⋅ 101 ⋅ 137
Durch Kombinationen dieser Primfaktoren können weitere Teiler der achtstelligen Zahl durch Multiplikation berechnet werden:
7373 = 73 ⋅ 101
13837 = 101 ⋅ 137
10001 = 73 ⋅ 137
... usw.
Der Zauberer muss als vor der Vorführung des Tricks nichts weiteres tun als die Zahlen 73, 101, 137, 7373, 13837, usw. auswendig lernen, denn sie sind Teiler einer jeden wie oben gebildeten achtstelligen Zahl.
Variante:Ein Zuschauer wählt eine beliebige dreistellige Zahl. Diese wird - wie oben - zweimal hintereinander notiert wird, sodass eine sechsstellige Zahl entsteht. Nun geht der Zauberer eine Wette mit dem Zuschauer ein: Der Zuschauer erhält den Rest, der sich bei der Division mit der magischen Zahl 7 ergibt, in Euro als Gewinn ausbezahlt.

Zum Erstaunen der Zuschauer ist jede so gebildete Zahl durch 7 teilbar. Es muss also kein Gewinn ausbezahlt werden!
Erklärung:
Das zweimalige Hintereinander-Schreiben zu einer sechstelligen Zahl entspricht einer Multiplikation mit der Zahl 1001. Hier:
675 ⋅ 1001 = 675675
Da nun 7 eine Teiler von 1001 (ebenso wie 11 und 13) ist, ist also jede so gebildete sechsstellige Zahl durch 7 teilbar. Der Zauberer hat also Glück und muss wohl nie einen Gewinn ausbezahlen; es sei denn, er hat sich verrechnet!

Aufgaben zu den Teilbarkeitsregeln:
Aufgabe 1: Untersuchung auf TeilbarkeitAufgaben zu Teilermengen und Primfaktoren:
Aufgabe 6: Teilermenge und PrimfaktorzerlegungAufgaben zu gemeinsamen Vielfachen und Teilern:
Aufgabe 11: Gemeinsame VielfacheVermischte Aufgaben:
Aufgabe 16: Taschenrechner