
 |
Graphen |
|
Als eigenständiges Teilgebiet der Mathematik ist die Graphentheorie, bei der es um Eigenschaften und Beziehungen in netzartigen Strukturen aus Kanten und Knoten geht, noch sehr jung. Entwicklungen von elektrischen Schaltungen und genauere Untersuchungen von chemischen Verbindungen führten in der Mitte des 19. Jahrhunderts zu einem Bedarf nach einer eigenständigen Theorie über Graphen. Solche Graphen findet man heute in Straßennetzen, Computernetzwerken, Versorgungsnetzen, Schaltkreisen und sozialen Beziehungen. Dabei geht es sehr häufig um Optimierungsaufgaben. Wie findet man den schnellsten Weg zwischen zwei Orten? Wie kann man ein schnelles Computernetz aufbauen? Wie kann man eine kostengünstige Postzustellung oder Abfallentsorgung organisieren? Wer ist mit wem befreundet?
Aufgrund dieser zahlreichen Anwendungen spielt die schnell wachsende Graphentheorie auch eine herausragende Rolle in der theoretischen Informatik, die mit Hilfe von Algorithmen die abstrakte Struktur der Netze genauer untersucht.
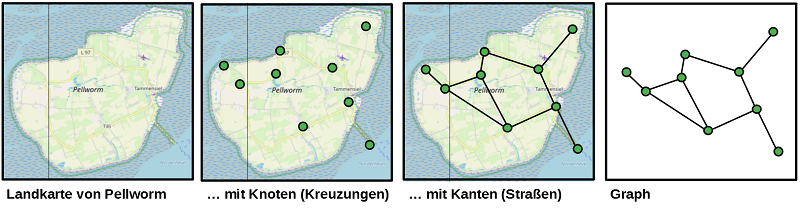
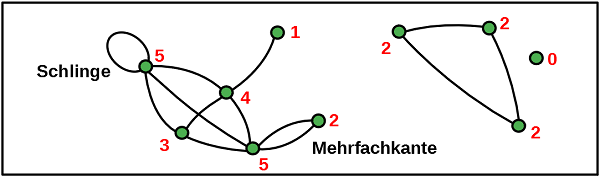
Unter einem Graphen versteht man ein netzartiges Gebilde, das aus Knoten (auch Ecken genannt) und Kanten besteht. Dabei verbindet jede Kante zwei Knoten oder eine Kante einen Knoten mit sich selbst. Dann entsteht eine "Schlinge". Von einem Knoten dürfen auch mehrere Kanten ausgehen, es darf aber auch Knoten geben, von der keine Kanten ausgeht. Es ist nicht notwendig, dass die Kanten als gerade Strecken eingezeichnet werden, sie dürfen durchaus auch gebogen sein.
Sind zwei Knoten durch mehrere Kanten verbunden, so spricht man von Mehrfachkanten. Dann hat man es mit einem Multigraphen zu tun. Einfache Graphen haben keine Mehrfachkanten.
Kann man von jedem Knoten zu jedem anderen Knoten entlang von Kanten gelangen, so heißt der Graph zusammenhängend. Ein nicht zusammenhängender Graph kann aus Teilen bestehen, die jeder für sich wieder zusammenhängend ist. Diese Teile nennt man dann Komponenten des Graphen.
Der einfache Graph des Straßennetzes von Pellworm hat also 9 Knoten, 10 Kanten und ist zusammenhängend. Schlingen und Mehrfachkanten sind nicht vorhanden. Der unten abgebildete Graph hingegen zeigt einen Multigraphen mit Schlinge. Von einem Knoten gehen keine Kanten aus. Er besteht aus mehreren Komponenten.
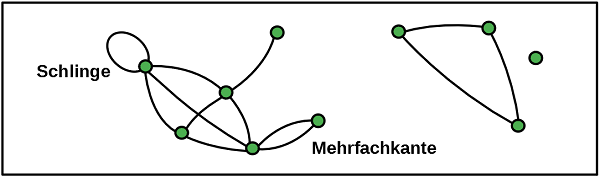
Denkt man an die Straßennetze in manchen Innenstädten, so ist der Straßenverkehr dort häufig durch Einbahnstraßen geregelt. Verbindungen zwischen zwei Knoten können dann nur in eine Richtung durchlaufen werden. Um die Richtung zu verdeutlichen ersetzt man die Kanten im Graphen durch Pfeile. Graphen, in denen alle Kanten eine Richtung haben, nennt man gerichtete Graphen oder auch Digraphen (vom englischen: „directed graph“).
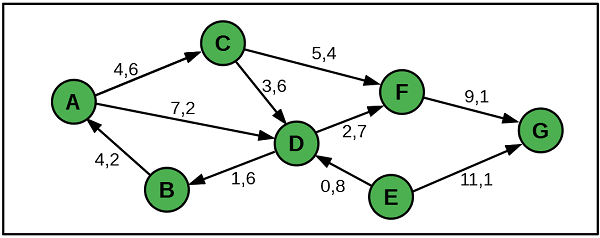
Will man den kürzesten Weg zwischen zwei Orten in einen Straßennetz finden, so müssen natürlich die Entfernungen zwischen den einzelnen Knoten des zugehörigen Graphen bekannt sein. Jeder Kante des Graphen wird also eine Zahl, hier die Entfernung zugeordnet. Die Kanten werden also bewertet (gewichtet) und man erhält einen bewerteten (gewichteten) Graphen. Das Beispiel zeigt einen gerichteten bewerteten Graphen, bei dem die Knoten mit Großbuchstaben bezeichnet sind:
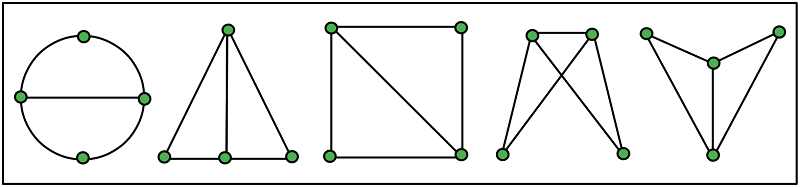
Immer wieder kommt es vor, dass zwei Graphen zwar unterschiedlich aussehen können, aber dennoch irgendwie das gleiche Netzwerk darstellen. Dazu müssen die beiden Graphen in ihrer Anzahl an Knoten, ihrer Anzahl an Kanten und auch in ihren Verbindungen untereinander genau übereinstimmen. Die beiden Graphen sind dann zwar nicht „gleich“, aber irgendwie stehen sie in einer sehr engen Beziehung zueinander. Man sagt dann, die Graphen sind zueinander isomorph. Sind zwei Graphen zueinander isomorph, dann ist es theoretisch möglich, die beiden Graphen durch Verschieben der Knoten und Verbiegen, Dehnen und Zusammenziehen der Kanten die beiden Graphen genau übereinander zu legen. Die Kanten müssen dabei beim Verschieben mit ihren Knoten verbunden bleiben. Verboten ist es auch, Kanten durchzuschneiden oder neu zu verknoten.
Die fünf Graphen unten sind alle zueinander isomorph. Sie sehen auf den ersten Blick zwar alle unterschiedlich aus, sie beschreiben aber alle das „gleiche“ Gefüge aus Knoten und Kanten.
Für die Arbeit mit Graphen ist ein weiterer wichtiger Begriff nötig: Die Ordnung (auch Grad oder Knotengrad) eines Knotens ist die Anzahl der Kanten, die von einem Knoten ausgehen. Ein alleinstehender Knoten hat also die Ordnung 0. Wie werden aber Schlingen gezählt? Nach Festlegung werden beide Enden der Schlinge einzeln gezählt. Jede Schlinge vergrößert also die Ordnung eines Knoten um 2. In folgenden Beispiel ist jeweils die Ordnung des Knoten rot angegeben:
Für die Arbeit mit Graphen am Computer sind die bildlichen Darstellungen von Graphen mit Knoten und Kanten wie in den bisherigen Beispielen nicht immer hilfreich. Eine gute Möglichkeit für die Arbeit mit Graphen am Computer sind Tabellen. Jeder Graph lässt sich in eine so genannte Nachbarschaftstabelle (oder auch Adjazenzmatrix) überführen. Dabei wird in jedes Feld der Tabelle die Anzahl der Kanten zwischen den beiden zugehörigen Knoten eingetragen. Ein Graph mit n Knoten hat also eine Adjazenzmatrix mit n2 Einträgen.
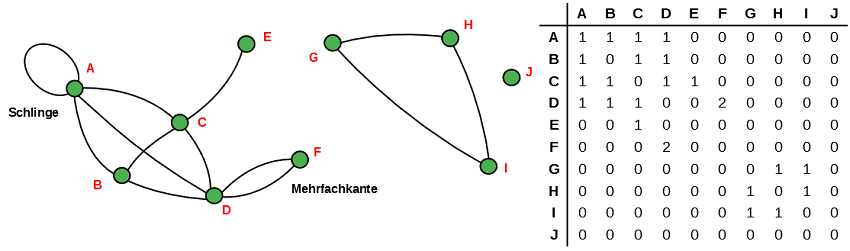
Mit ein wenig Übung kann man viele Eigenschaften eines Graphes anhand der Nachbarschaftstablle ablesen. Schlingen erkennt man an einem Eintrag in der Diagonalen und Mehrfachkanten an einem Eintrag, der größer als 1 ist. Bei isolierten Knoten sind alle Einträge in der zugehörigen Spalte oder Zeile 0.
Mit Hilfe von Nachbarschaftstabellen kann man auch gut untersuchen, ob zwei Graphen isomorph sind. Dann sind nämlich auch ihre Nachbarschaftstabellen identisch. Allerdings gibt es einen kleinen Haken. Zuvor müssen die entsprechenden Knoten mit den gleichen Buchstaben oder Namen bezeichnet werden. Hat man hierbei einen Fehler gemacht, so kann man diesen Fehler bei der Nachbarschaftstabelle durch Vertauschen von Zeilen und Spalten korrigieren.
Kantenzüge:Ein bekanntes Ferienziel im Sommer ist die Insel Föhr in der Nordsee. Sie gehört zu den Nordfriesischen Inseln und ist die größte und bevölkerungsreichste deutsche Insel. Die größte Stadt auf Föhr ist Wyk.
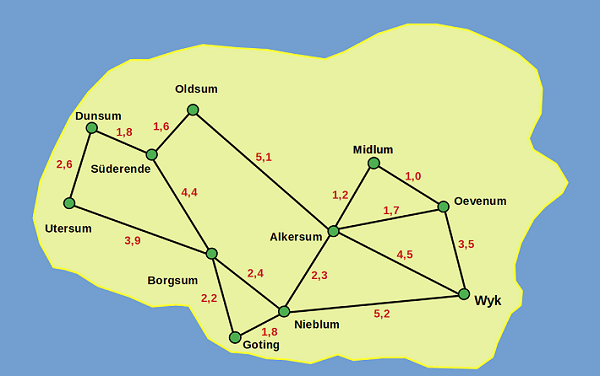
Problem 1: Auf der Insel Föhr hat es geschneit. Nun sollen die Straßen der Insel möglichst schnell vom Schneepflug geräumt werden. Ausgehend vom Depot des Schneepflugs in Wyk soll jede Straße genau einmal zur Zeitersparnis befahren werden. Zum Schluss soll der Schneepflug wieder in seinem Depot in Wyk ankommen. Ist eine solche Tour möglich?
Problem 2: Ein Gemüselieferant aus Wyk möchte alle Supermärkte von Föhr beliefern. In jeden Dorf befindet sich ein solcher Supermarkt. Um die Benzinkosten möglichst gering zu halten sucht er nun eine Route, die jeden Supermarkt genau einmal anfährt und möglichst kurz ist. Welche Route ist die kürzeste?
Beide Probleme beschreiben typische Fragestellungen aus dem Bereich der Graphentheorie. Beides Mal geht es um eine Folge aneinander stoßender Kanten. Man kann diese Folge nachzeichnen, ohne den Stift abzusetzen. Solche Folgen nennt man auch Kantenzüge. Im Allgemeinen ist es erlaubt, dieselbe Kante mehrfach in einen Kantenzug "einzubauen". Ebenso können auch Knoten im Allgemeinen mehrfach "angefahren" werden. Beachte: Eine einzelne Kante ist auch schon ein Kantenzug.
Bei Problem 1 stehen die Kanten selber im Vordergrund, bei Problem 2 hingegen sind die Knoten von besonderer Bedeutung. Algorithmen können nun solche Kantenzüge auch bei Graphen mit zahlreichen Kanten und Knoten finden und diese analysieren.
Eulersche Kantenzüge
Ein besonderer Kantenzug ist der sogenannte Eulersche Kantenzug. Ein solcher Kantenzug hat die folgenden Eigenschaften:
| • | Der Kantenzug enthält keine Kante doppelt oder mehrfach. |
| • | Sämtliche Kanten des Graphen kommen genau einmal im Kantenzug vor. |
Zusätzlich gilt: Wenn man bei einem Eulerschen Kantenzug zum Ausgangspunkt zurückkehrt, also wenn Start- und Endknoten identisch sind, so nennt man ihn geschlossen. Einen geschlossenen eulerschen Kantenzüge nennt man auch eine eulersche Tour. Bei alle anderen Eulerschen Kantenzüge spricht man von offenen eulerschen Kantenzügen. Es ist ebenso üblich, dass man Graphen, die einen geschlossenen eulerschen Kantenzug enthalten als eulersche Graphen zu bezeichnen. Solche Graphen kann man in einem Zug ohne Absetzen des Stifts zeichnen. Dabei wird keine Kante doppelt gezeichnet. Außerdem endet die Linie wieder im Ausgangsknoten.
Ein berühmtes Beispiel zum Thema Eulersche Kantenzüge findet man unter dem Stichwort "Königsberger Brückenproblem". In der Stadt Königsberg gibt es den Fluss Pregel. Seine Inseln unterteilen die Stadt in vier Stadtteile, die durch Brücken miteinander verbunden sind.
Nun zum Problem: Gibt es einen Weg durch die Stadt, bei dem man jede Brücke genau einmal überquert und ist es vielleicht sogar möglich, dass man wieder zum Ausgangspunkt zurückgelangt, sodass ein Rundweg entsteht?
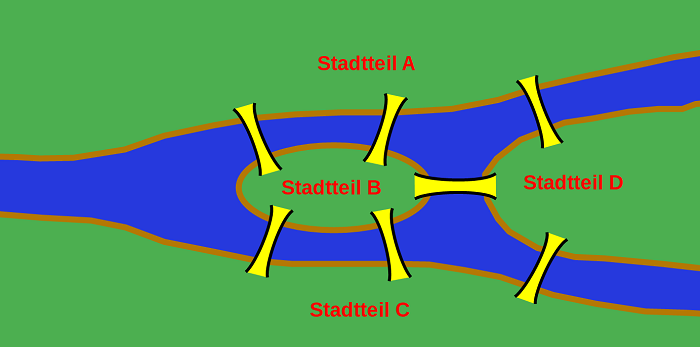
Das Problem ist mit Hilfe der Graphentheorie lösbar. Hierzu überführt man die Stadtkarte in einen abstrakten Graphen. Die Knoten des Graphen sind dabei die vier Stadtteile, die Brücken werden als Kanten dargestellt. Für die weitere Argumentation ist es hilfreich, wenn man gleich die Ordnung der Knoten notiert.
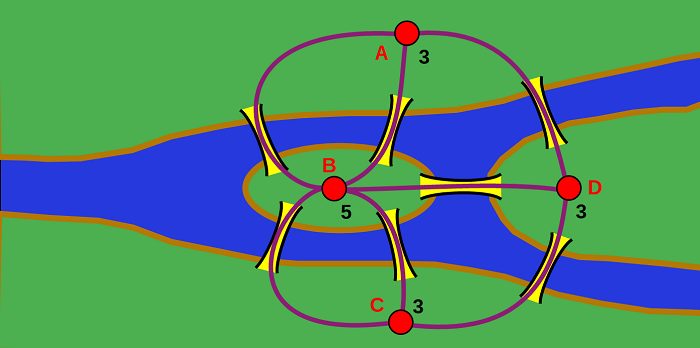
Leonhard Euler konnte 1736 beweisen, dass es keinen solchen Weg gibt. Entscheidend ist die Ordnung der Knoten. Beim Königsberger Brückenproblem hat jeder Knoten ungerade Ordnung. Betrachtet man beispielsweise einen Knoten im mittleren Teil eines Weges, so wird dieser Knoten über eine Kante erreicht. Weiterhin benötigt man wieder eine Kante um von diesem Knoten zum nächsten zu gelangen. Ein solcher Knoten müsste dann die Ordnung 2 haben, eine Kante zum Erreichen des Knotens und eine Kante zum Verlassen des Knotens. Selbstverständlich kann eine Knoten auch zweimal erreicht werden. Dann müsste dieser Knoten die Ordnung 4 haben. Allgemein muss also jeder Knoten im Mittelteil eines Weges eine ungerade Ordnung aufweisen.
Anders sieht es beim Ausgangs- und Endknoten aus. Hier können auch Knoten mit ungerade Ordnung auftreten. Damit ein eulerscher Kantenzug überhaupt möglich ist, dürfen also maximal 2 Knoten mit ungerade Ordnung im Graphen vorkommen. Diese beiden Knoten sind dann die Ausgangs- und Endknoten des Eulerschen Kantenzuges.
Für geschlossene Eulersche Kantenzüge, also Rundweg, bei denen man wieder zum Ausgangspunkt zurück gelangt, müssen alle Knoten ungerade Ordnung haben. Hier muss ja jeder Knoten erreicht und auch wieder verlassen werden.
In Königsberg kann es also keinen Weg, bei dem man jede Brücke genau einmal überquert geben. Auch ein solcher Rundweg ist unmöglich.
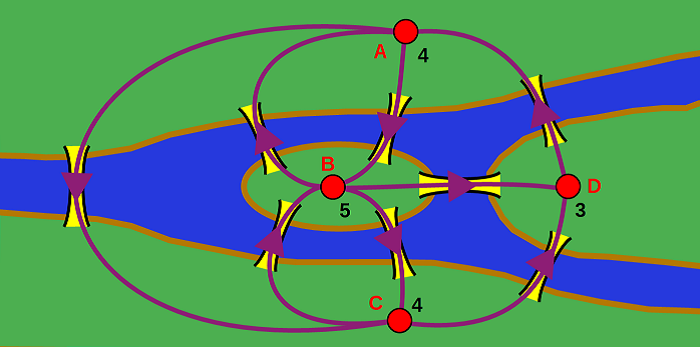
Anders sieht die Situation aus wenn man zum besseren Verständnis eine weitere Brücke in Königsberg hinzufügen könnte, und zwar von Stadtteil A zu Stadtteil C. Nun haben die Knoten A und C gerade Ordnung. Eulersche Wege sind nun möglich. Bei diesen Wegen müssen allerdings die Knoten B und D die Ausgangs- und Endknoten sein. Ein möglicher Weg ist unten eingezeichnet. Für die Reihenfolge der durchlaufenen Knoten ergibt sich:
B – D – A – B – A – C – B – C – D
Hamiltonsche Kantenzüge
Im Gegensatz zu den Eulerschen Kantenzügen liegen im Folgenden nun nicht mehr die Kanten eines Graphen im Vordergrund, sondern die Knoten. Bei einem Eulerschen Kantenzug kam es darauf an, dass man jede Kante genau einmal "durchläuft", bei einem sogenannten Hamiltonschen Kantenzug hingegen kommt es darauf an, dass man jeden Knoten genau einmal „durchläuft“. Wichtig ist, dass jeder Knoten nicht mehr als einmal enthalten sein darf. Außerdem braucht nicht jede Kante des Graphen enthalten sein.
Ist ein Hamiltonscher Kantenzug zusätzlich geschlossen, kehrt man also wieder zum Ausgangsknoten zurück, so spricht man von einem Hamiltonschen Kreis.
Es ist schon sehr erstaunlich, dass man noch kein Kriterium gefunden hat, wie man schnell entscheiden kann, ob es in einem gegebenen Graphen einen Hamiltonkreis gibt. Ebenso gibt es noch kein Verfahren, wie man einen Hamiltonkreis am besten findet. Nach wie vor sind das Fragen der aktuellen Forschung. Eins ist jedoch sicher: Je mehr Kanten ein Graph hat, desto leichter ist es, einen Hamiltonschen Kreis zu finden.
Ein mathematisches Problem im Zusammenhang mit Hamiltonkreisen findet man oft unter dem Begriff "Travelling Salesman Problem". Dabei geht es beispielsweise um einen Geschäftsmann aus Kassel, der Kunden in verschiedenen Städten München, Berlin und Dortmund vor Ort beraten möchte. Nun möchte er seine Geschäftsreise so planen, dass er jede Stadt genau einmal besucht und die Gesamtstrecke natürlich möglichst gering ist. Die Entfernungen zwischen den Städten sind in der Tabelle aufgelistet, der zugehörige Graph ist ebenso dargestellt:
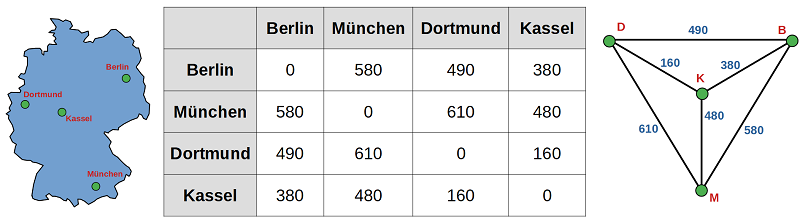
Insgesamt gibt es 6 verschiedenen Routen von Kassel aus, wobei jeweils 2 die gleiche Gesamtlänge haben. Sie unterscheiden sich lediglich in der Richtung, in der man die Route durchfährt.

Der Geschäftsmann sollte sich also zuerst auf den Weg nach München machen und dann von dort über Berlin und Dortmund zurück nach Kassel fahren. Mit 1710 km ist das die kürzeste Route.
Abschlussbemerkung:
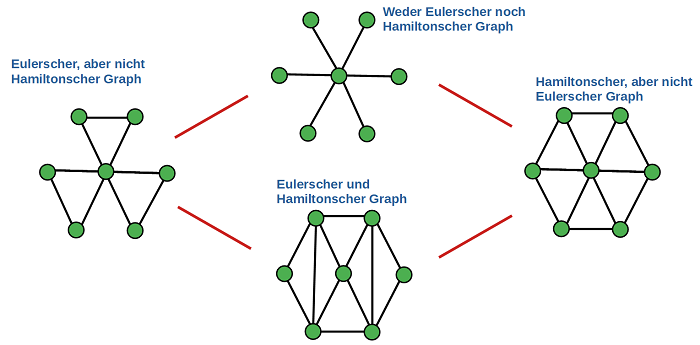
Eulersche Graphen und Hamiltonsche Graphen sind verschiedene Dinge. Es gibt Graphen, in denen man geschlossen Eulersche Kantenzüge und geschlossene Hamiltonsche Kantenzüge findet. Es gibt aber auch Graphen, in denen man zwar Eulersche Kreise aber keine Hamiltonsche Kreise findet, und umgekehrt. Natürlich findet man auch Graphen, die weder Eulersche Graphen noch Hamiltonsche Graphen sind. Das Beispiel zeigt diese Unterschiedlichkeit:

Aufgaben zu Graphen:
Aufgabe 1: GrundbegriffeAufgaben zu Kantenzügen:
Aufgabe 6: Eulersche Kantenzüge