Eine natürliche Zahl n soll mit Hilfe eines Algorithmus untersucht werden, ob sie eine Primzahl ist oder nicht.
Zur Erinnerung: Eine natürliche Zahl n ist genau dann eine Primzahl, wenn sie einerseits größer als 1 ist und andererseits nur sich selbst oder 1 als Teiler hat (Beispiele sind: 2, 3, 5, 7, 11, …). Wichtig: Eine natürliche Zahl t nennt man Teiler von n, wenn der Quotient n/t eine natürliche Zahl ist.
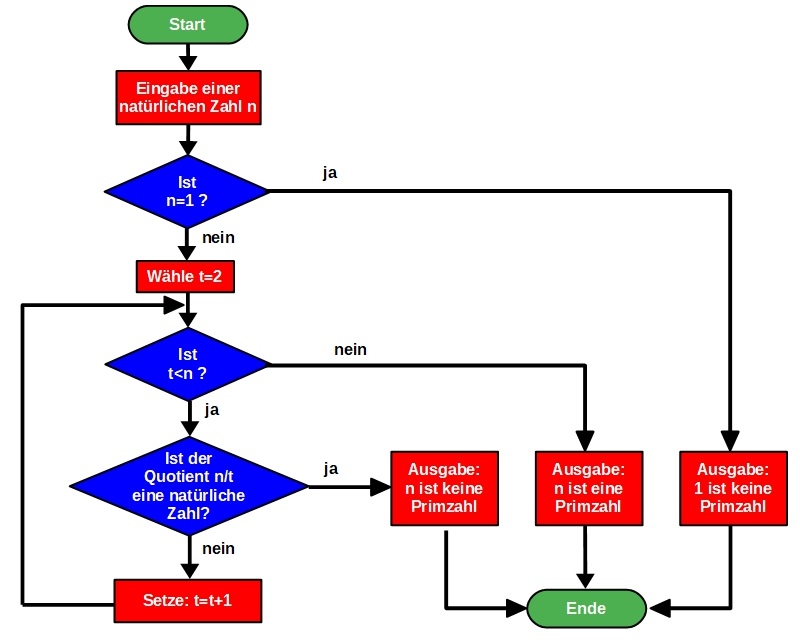
Das Flussdiagramm veranschaulicht die Struktur eines möglichen Programms, das entscheiden kann, ob eine natürliche Zahl n Primzahl ist, oder nicht!

| a) | Beschreibe in Worten die Funktionsweise dieses Programms! |
| b) | Im Programm ist eine Schleife eingebaut. Kennzeichne die Bereiche im Flussdiagramm, die zu der Schleife gehören! |
| c) | Im Flussdiagramm ist die Verzweigung mit der Frage: "Ist t < n?" eingezeichnet! Warum ist diese Verzweigung für eine einwandfreie Durchführung des Programms wichtig? |