
 |
Logik |
|
Die Logik – aus dem altgriechischen auch als „Folgerichtigkeit“ übersetzt – ist nicht nur ein Teilgebiet der Mathematik, sondern beschäftigt sich ganz allgemein mit dem „Schlussfolgern“. Dabei werden Argumente und Schlüsse formal und abstrakt auf ihre Gültigkeit untersucht. Der Inhalt der Aussagen steht dabei nicht im Vordergrund, wichtig ist die Frage, ob ein daraus abgeleiteter Schluss gültig ist. Ein simples Beispiel kann dies verdeutlichen:
Aus der Aussage: „Alle Schwaben sind Menschen“ kann nicht auf die Umkehrung „Alle Menschen sind Schwaben“ geschlossen werden. Nach der Logik ist dieser Schluss ungültig.
In der mathematischen Logik untersucht man nun solche Schlussfolgerungen auf ihre Gültigkeit. Dazu verwendet man eine komplizierte formale Sprache aus eigenen Zeichen und Symbolen. Dabei bildet die formale Logik nicht nur einen wichtigen Grundpfeiler für die Mathematik, sondern auch für die theoretische Informatik.
Aussagenlogik:Innerhalb der Aussagenlogik beschäftigt man sich mit Aussagen, die miteinander verknüpft werden. Im üblichen Sprachgebrauch sind Aussagen häufig nicht scharf und präzise formuliert, so dass man nur schwer entscheiden kann, ob eine Aussage wahr oder falsch ist. Meistens wären in diesen Fällen Zusatzinformation nötig, die man aber all zu oft nicht kennt. Bei Sprechen besteht natürlich immer die Möglichkeit, solche Zusatzinformationen zu erfragen. Außerdem stehen Aussagen immer in einem Kontext, sodass Missverständnisse vermieden werden können. Gestik und Mimik im Dialog unterstützen ebenso die Gültigkeit von Aussagen, sodass weitgehende Einigkeit zwischen den Gesprächspartner erzielt werden kann. Beispiel:
Die Aussage "Dieser Pulli ist sehr bequem!" ist sehr unpräzise! Welcher Pulli ist gemeint? Was genau bedeutet "bequem"? Ab wann ist ein Pulli "sehr" bequem? Ist das nicht für jeden Träger unterschiedlich? Der eine findet in "bequem", der andere nicht! In einem Kontext unter Freunden ist vermutlich die Aussage "verständlich", zur mathematisch, formalen Untersuchung auf ihre Gültigkeit eignet sich diese Aussage in dieser Form eher nicht.
In der Mathematik hingegen sind solche Unschärfen nicht gewünscht. Zum Glück hat man mathematische Begriffe genau, präzise und unmissverständlich definiert. In einem solchen System lassen sich nun Aussagen formulieren und auf ihren Wahrheitsgehalt untersuchen:
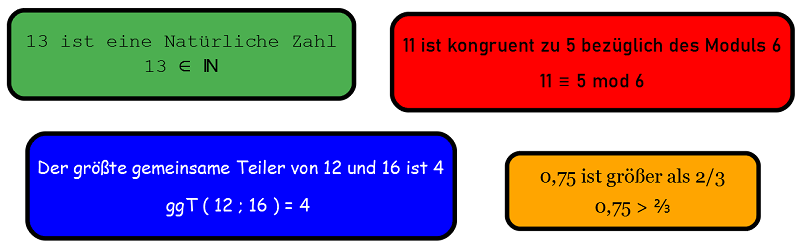
Aussagen sind zu unterscheiden von reinen mathematischen Begriffen oder Objekten wie etwa 3,14876234 oder 3 mod 5 oder f(x). Diese können nicht auf ihren Wahrheitsgehalt untersucht werden.
Verschiedene Aussagen lassen sich miteinander verknüpfen. In der Aussagenlogik untersucht man diese Verknüpfungen. Anhand der beiden Aussagen A: "Es regnet" und B: "Ich habe einen Regenschirm" lassen sich einige Verknüpfungen sehr gut verdeutlichen.
Es regnet und ich habe einen Regenschirm.
Es regnet oder ich habe einen Regenschirm.
Wenn es regnet, dann habe ich einen Regenschirm.
Wenn es nicht regnet, dann habe ich keinen Regenschirm.
Wenn ich keinen Regenschirm habe, dann regnet es auch nicht.
Es regnet genau dann wenn ich einen Regenschirm habe.
Wie die Beispiele zeigen wurden die Einzelaussagen von ihrer Aussagekraft nicht verändert, sondern nur in verschiedene logische Zusammenhänge gesetzt. Dazu waren natürlich gewisse sprachliche und grammatikalische Anpassungen notwendig. Beim ersten Beispiel hat man die beiden Aussagen mit einem "und" verknüpft. Ist die Aussage A wahr ("Es regnet") und ist die Aussage B wahr ("Ich habe einen Regenschirm"), so darf man in diesem Fall nach der mathematischen Logik schließen, dass auch die Verknüpfung von A und B (Es regnet und ich habe einen Regenschirm) zulässig ist.
Achtung:
Setzt man einzelne Satzbausteine aus den beiden obigen Aussagen A und B neu zusammen, so entstehen völlig neue Aussagen, wie etwa "Es regnet Regenschirme". Das ist aber keine logische Verknüpfung im Sinne der mathematischen Logik sondern nur ein Zusammensetzen von gegebenen Wörtern. Es ist hier nicht möglich, aus den Wahrheitsgehalten der Einzelaussagen auf die Gültigkeit die neuen Aussage zu schließen.
Die Grundverknüpfungen und ihre Wahrheitstabellen:In der Aussagenlogik kann man jeder Aussage genau einen der beiden möglichen Wahrheitswerte zuordnen. Die Aussage "Es regnet" kann also "falsch" sein, dann erhält diese falsche Aussage den Wahrheitswert "0". Ist die Aussage hingegen "wahr", so ordnet man der Aussage den Wahrheitswert "1" zu. Diese Wahrheitswerte können in eine Tabelle, der so genannten Wahrheitstabelle eingetragen werden. Hier ist ein Beispiel mit mathematischen Aussagen:
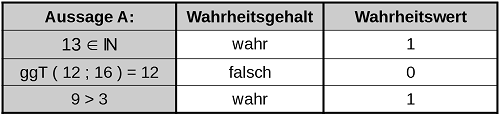
Die Negation (Verneinung):
Jede Aussage kann negiert (verneint) werden. Dabei muss man darauf achten, dass man auch genau die gegenteilige Aussage formuliert. Beim Negieren wird natürlich der Wahrheitswert umgekehrt (verkürzt geschrieben: " A ", auch " NOT A "). Das kann man gut an der folgenden Tabelle erkennen:

Die Konjunktion:
Werden zwei elementare Aussagen A: "Es regnet" und B: "Ich habe einen Regenschirm" mit einem "und" verknüpft, so spricht man von einer Konjunktion (verkürzt geschrieben: " A ˄ B ", auch " A AND B "). Die Verknüpfung der beiden Aussagen "A und B" ist genau dann wahr, wenn beide Einzelaussagen A und B wahr sind und genau dann falsch, wenn eine der beiden Aussagen A oder B falsch ist. Diesen Zusammenhang kann man gut in einer Wahrheitstabelle veranschaulichen. Auf der linken Seiten werden dabei in den grau unterlegten Felder alle Kombination der beiden Wahrheitswerte vorgegeben.

Die Disjunktion:
Man kann die elementaren Aussagen auch mit einem "oder" verknüpfen. In diesem Fall spricht man von einer Disjunktion (verkürzt geschrieben " A ˅ B ", auch " A OR B "). Mindestens eine der beiden Aussagen A oder B muss also erfüllt sein, sodass die verknüpfte Aussage wahr ist. Die verknüpfte Aussage "Es regnet oder ich habe einen Regenschirm" ist also dann wahr, wenn es entweder regnet oder ich einen Schirm dabei habe oder beides. Die Wahrheitstabelle sind dann folgendermaßen aus:

Diese logischen Verknüpfungen Negation, Konjunktion und Disjunktion bilden die Grundverknüpfungen der Aussagenlogik. Aus diesen Grundverknüpfungen können weitere Verknüpfungen zusammengesetzt werden.
